Science
Explore a universe of black holes, dark matter, and quasars... A universe full of extremely high energies, high densities, high pressures, and extremely intense magnetic fields which allow us to test our understanding of the laws of physics.
- Astronomer's Toolbox - A look at the tools and methods scientists use to study the high energy universe.
- Objects of Interest - The universe is more than just stars, dust, and empty space. Explore some of the objects that make up our universe, from our own Sun to distant pulsars and black holes.
- Big Questions - Scientific discoveries often reveal new mysteries. Take a look at a few of the mysteries that astronomers and astrophysicists are working on right now.
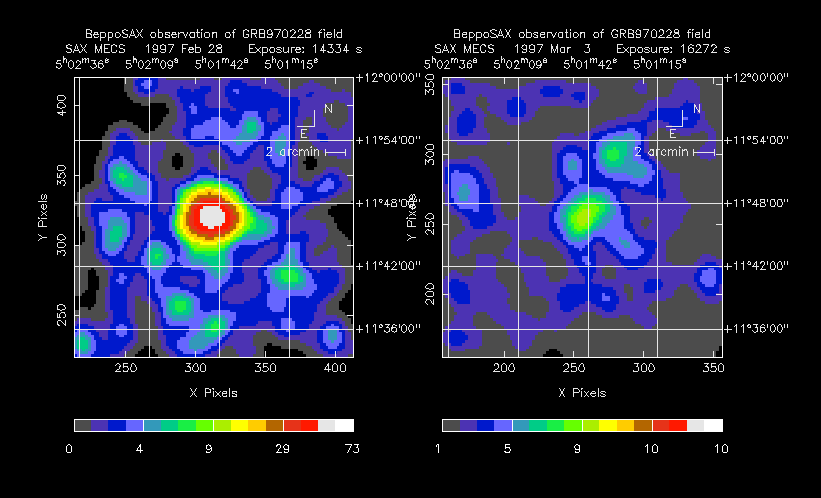
- Featured Science - Special objects and images in high-energy astronomy.