Newton's Law of Gravitation

Duration
1-2 class periods
Essential Questions
- How do the acceleration and force due to gravity depend on the radius and mass of a planet?
- How does the mass of a falling body affect the rate at which it falls in a gravitational field?
Objectives
Students will:
- see that the acceleration of an object due to gravity is independent of its mass.
- determine what they would weigh on other planets.
- see that the force they feel from gravity depends on the radius and the mass of the planet.
Science Concepts
- Newton's Law of Gravitation states that two objects with masses m1 and m2, with a distance r between their centers, attract each other with a force F given by: F = Gm1m2/r2, where G is the Universal Gravitational Constant (equal to: 6.672x10-11Nm2/kg2).
- Objects near the surface of the Earth fall at the same rate independent of their masses.
- The force of gravity on different planets is different, depending on their mass and radius.
About this Poster
The Swift Gamma-Ray Burst Explorer is a NASA mission that is observing the highest energy explosions in the Universe–gamma-ray bursts (GRBs). Launched in November, 2004, Swift is detecting and observing hundreds of these explosions, vastly increasing scientists' knowledge of these enigmatic events. Education and public outreach (E/PO) is also one of the goals of the mission. The NASA E/PO Group at Sonoma State University develops classroom activities inspired by the science and technology of the Swift mission, which are aligned with the national Standards. The front of the poster illustrates Newton's Law of Gravitation, and descriptions of the drawings can be found on the next page. This poster and activity are part of a set of four educational wallsheets which are aimed at grades 6-9, and which can be displayed as a set or separately in the classroom.
The activity below provides a simple illustration of Newton's Law of Gravitation. The activity is complete and ready to use in your classroom; the only extra materials you need are listed on p. 4. The activity is designed and laid out so that you can easily make copies of the student worksheet and the other handouts.
The NASA E/PO Group at Sonoma State University:
- Prof. Lynn Cominsky: Project Director
- Dr. Phil Plait: Education Resource Director
- Sarah Silva: Program Manager
- Tim Graves: Information Technology Consultant
- Aurore Simonnet: Scientific Illustrator
- Laura Dilbeck: Project Assistant
We gratefully acknowledge the advice and assistance of Dr. Kevin McLin, the NASA Astrophysics division Educator Ambassador (EA) team, and the WestEd educator review panel. This poster set represents an extensive revision of the materials created in 2000 by Dr. Laura Whitlock and Kara Granger for the Swift E/PO program.
The Swift Education and Public Outreach website: https://imagine.gsfc.nasa.gov/educators/programs/swift/
This poster and other Swift educational materials can be found at: https://imagine.gsfc.nasa.gov/educators/programs/swift/
National Science Education Standards and Mathematics Standards for the set of four Newton's Law wallsheets can be found at: https://imagine.gsfc.nasa.gov/educators/programs/swift/classroom/newtons_laws_standards.html
Description of the Front of the Poster
- Solar system
- All the planets in the solar system orbit the Sun due to its gravity. The inner planets are closer to the Sun and feel more gravity, so as a result they move faster.
- Astronaut
- Gravity goes on forever; an astronaut in orbit is accelerated by Earth's gravity. But without the balancing upward force from the ground, she falls freely. Some people call this "weightlessness", but that's not really true. "Free fall" is a better term.
- Newton
- Isaac Newton was the person who realized that all massive objects in the Universe apply the force of gravity to all other massive objects. An apple didn't really fall on his head, but he did realize that the force causing an apple to fall is the same as the force causing the Moon to orbit the Earth – the Earth's gravity.
- Girl falling
- While falling, a girl feels a brief period of "free fall" while she is in the air because the Earth's gravity is not balanced by any upwards force. The gravity due to the girl's mass applies the same force on the Earth as the Earth's gravity does on the girl, but because the Earth has so much more mass it does not accelerate very much at all, while the girl accelerates rapidly.
- Bike
- Bicyclists climbing a hill – or speeding down one – are certainly aware of gravity!
- Swift orbiting Earth
- The effect of Swift's horizontal velocity (from its launch rocket) exactly cancels the downward velocity gained from the acceleration due to Earth's gravity. This gives Swift its circular path around the Earth. See "Newton's law of Gravitation and the Swift Satellite" below.
Background Information for Teachers
It is well-known today that the force of gravity an object feels depends on a relatively simple relationship: F= GmM/r2, where F is the force of gravity, M is the mass of one object, m is the mass of a second object, r is the distance between them, and G=6.672 x 10-11Nm2/kg2 is a constant called Newton's Universal Gravitational Constant.
This relationship governs the motion of the planets in their orbits, guides spacecraft to their destinations, and even keeps our feet firmly on the ground. Sir Isaac Newton derived this equation in the 17th century but it is still useful today.
When you teach students science, they love to ask, "How does this affect me?" For once, you can answer this honestly: this directly affects them. It affects everything! In fact, we can use Newton's equation to figure out just how hard the Earth is pulling us.
Look again at the equation.
We know that F = ma from Newton's Second Law of Motion. We can set that equal to the equation above, and solve for a, the acceleration due to Earth's gravity:
a = G ME / RE2
where ME is the mass of the Earth and RE is its radius. We know the values of all these numbers:
G = 6.672 x 10-11 N m2/kg2
ME = 5.96 x 1024 kg
RE = 6375 km
The derivation of Newton's Law of Gravitation is beyond the scope of this activity. However, if you want to see it, it can be found on the Swift site: https://imagine.gsfc.nasa.gov/educators/programs/swift/classroom/law_grav_derivation.html
Substituting those into the equation above, we see that the acceleration due to gravity for any object on the Earth's surface (usually called g or "little g") is 9.8 m/sec2. In other words, an object dropped near the Earth's surface will accelerate 9.8 m/sec for every second it falls: it will move at a velocity of 9.8 m/s after the first second, 2 x 9.8m/sec = 19.6 m/sec the next, 3 x 9.8m/sec = 29.4 m/sec the next, and so on.
This equation has a very important implication: the mass of the object falling doesn't matter! A grape and a grand piano will both fall at the same acceleration, and therefore the same velocity (if they both drop from the same height). This is counter-intuitive to most people, including, most likely, your students. Our intuition tells us that more massive objects fall faster, but that is not correct.
Students may be confused by this because they know that more massive objects weigh more. While this is true, it is important to distinguish between weight and mass. Mass is intrinsic to matter, but weight is the force of gravity on that mass. Remember, F=ma. The acceleration due to gravity does not depend on the mass of the object falling, but the force it feels, and thus the object's weight, does.
This tells us two things. One is that the speed at which an object falls does not depend on its mass. The second is that if the acceleration due to gravity were different (say, on another planet) you'd weigh a different amount. These two concepts are the basis of the classroom activities.
Additional Background Information for Teachers
Sir Isaac Newton (1642-1727) established the scientific laws that govern 99% or more of our everyday experiences. He also explained our relationship to the Universe through his Laws of Motion and his Universal Law of Gravitation. These are considered by many to be the most important laws in all physical science.
Newton was the first to see that such apparently diverse phenomena as an apple falling from a tree, the Moon orbiting the Earth, and the planets orbiting the Sun operate by the same principle: force equals mass multiplied by acceleration, or F=ma.
Our everyday lives are influenced by different forces: for example, the Earth exerts a force on us that we call gravity. We feel the force required to lift an object from the floor to a table. But how exactly does Newton's Second Law of Motion relate to gravity? To understand Newton's Law of Gravitation, you must first understand the nature of force and acceleration when applied to circular motion, rather than motion in a straight line.
Newton's First Law of Motion tells us that, without the influence of an unbalanced force, an object will travel in a straight line forever. This means that an object traveling in a circular path must be influenced by an unbalanced force. The circulating object has a velocity that is constantly changing, not because its speed is changing, but because its direction is changing. A change in either the magnitude (amount) or the direction of the velocity is called acceleration. Newton's Second Law explains it this way: A net force changes the velocity of an object by changing either its speed or its direction (or both.)
Therefore, an object moving in a circle is undergoing acceleration. The direction of the acceleration is toward the center of the circle. The magnitude of the acceleration is
a= v2/r
where v is the constant speed along the circular path and r is the radius of the circular path. This acceleration is called centripetal (literally, "center-seeking") acceleration. The force needed to produce the centripetal acceleration is called the centripetal force, Fcent = macent, according to Newton's Second Law. So therefore the centripetal force can be written as
align="center">Fcent= macent = mv2/r
Majestic examples of circular motion can be found throughout our Universe: Planets orbit around the Sun in nearly circular paths; moons orbit around their planets in nearly circular paths; and man-made satellites (such as Swift) can orbit the Earth in nearly circular paths.
Pre-Activity Reading
Newton's Law of Gravitation and the Swift Satellite
In our previous Newton's Law posters, we examined what happened when Swift was launched in the rocket and what happens as the rocket burns its fuel. We also studied the forces acting on Swift as it went into orbit. In this final poster we will study the relationship between the gravitational force on Swift and its acceleration and velocity.
Recall that as Swift enters its orbit, it has velocity that is purely "horizontal" – that is, it is moving parallel to the curved surface of the Earth at each point. However, the force of the Earth's gravity on Swift is "vertical" – pointed towards the center of the Earth. Why then does Swift not fall to Earth immediately? The answer is that Swift moves horizontally at just the right rate so that as it falls vertically, its motion creates a circular path around the Earth. This balance between "horizontal" and "vertical" motion is what is meant by "being in orbit." Swift will be able to stay in orbit for many years, as long as its horizontal velocity is maintained at a high enough rate. The special relationship between the horizontal velocity and the gravitational acceleration for any body that is orbiting another more massive body was worked out by Johannes Kepler years before Sir Isaac Newton figured out the Law of Universal Gravitation.
Eventually, the cumulative effect of the small number of atmospheric molecules hitting Swift in its orbit 600 km above Earth will cause the "horizontal" motion of the satellite to slow down; its horizontal motion will no longer be able to completely counteract its vertical motion. When this happens, Swift's orbit will start to "decay." As Swift spirals in closer to the Earth there will be even more atmospheric drag, which will cause Swift's orbit to decay increasingly faster. Swift will end its life plunging in through the Earth's atmosphere, probably sometime around 2014.
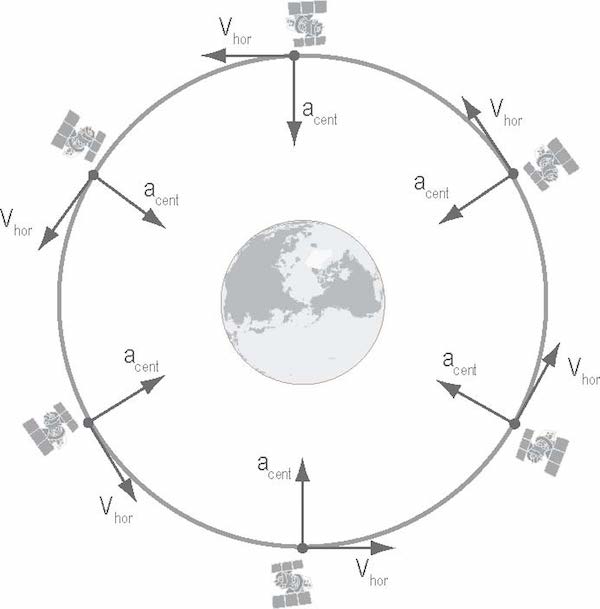
The relationship between the velocity and acceleration of Swift in its orbit (not to scale).
Procedure for In Class Activities
In these two activities, your students will investigate Newton's Law of Gravitation. In the first activity, you can divide them into teams to experimentally investigate the fact that the acceleration of an object due to gravity is independent of its mass. In the second activity (for advanced students), they can work individually or in pairs to calculate how their weight would change on other bodies in the solar system, and to see that the force due to gravity, and hence their weight, depends on the radius and mass of the planet.
Materials
- Several objects of different masses and sizes, such as pencils, crumpled up aluminum foil, coins, fishing weights, etc. Make sure they are not breakable!
- Calculator
Part A: The Fall of Man
Your students will be dropping various objects to the floor to see if they fall at different rates. Go over the background material to the level you think is appropriate for your class, but do not go over the concept that acceleration is independent of the mass of the falling object! They will find this out for themselves in the first part of the activity. When you give them materials to test, make sure they have different sizes, masses, and densities. Make sure they are not breakable! Also, make sure they won't be affected too much by air resistance; a balloon or a piece of paper won't work (although crumpled paper will if it is wadded up tightly).
After this activity, discuss the results with the students. Most likely, they will have predicted that the heavier object will hit first and found that this is not true; the two objects fell together at the same rate. Explain to them that this is because the acceleration due to gravity is independent of mass. Some students may have a hard time internalizing this. They may even disagree with the results. If that happens, demonstrate the activity for them again from a higher elevation (standing on a chair, for example), using very different mass objects (like a pencil and a heavy weight).
Part B: The Gravity of the Situation (Advanced Students)
Before doing Part B, remind them of the difference between acceleration and force. Go over Newton's law of gravitation, and stress the idea that the acceleration due to gravity on a planet's surface depends on the planet's size and mass, and that this means that they would have different weights on different planets. Review the derivation of "little g" that is given in the background information, and perhaps work one example for a different planet, so that they will understand how to proceed. You may also wish to use the questions in the box "Think About It!" as the basis for class discussion after the table is completed.
The students might be a little confused over the units for all these numbers (like G = 6.672x10-11 N m2/kg2). This is understandable! If they get confused, tell them that to complete the activity they only need to worry about the values of the numbers. The units are important when doing science, but for now they can just use the numbers.
Extension Activity - Swift Orbit (Advanced students)
The following activity is beyond the normal scope of this poster, but may interest advanced students. It may help to let them read the derivation of Newton's Law of Gravitation at: https://imagine.gsfc.nasa.gov/educators/programs/swift/classroom/law_grav_derivation.html. You might have to explain the math to them first.
- Use Kepler's Law: T2= K R3 to calculate the period of the Swift satellite in its 600 km orbit around the Earth. The period, T, is how long it takes for Swift to orbit once around the Earth. Remember that the distance, R, in this equation is measured from the center of the Earth, and that the Earth's radius is about 6375 km. The constant K in this equation is equal to (4π2) / (GME ), where ME is the mass of the Earth, and is equal to 5.96 x 1024 kg, and G is the gravitational constant: G = 6.67x 10-11N m2/kg2.
- What is Swift's velocity in its orbit? Recall that v = 2πR/T.
- If Swift's weight in orbit is 1255 kg, (see "Think About It!" part "e" on p. 8) why then do we refer to astronauts orbiting the Earth as "weightless"?
Hint: Students may get stuck on Question c, where they try to think of things that may have thrown off their timing. The two largest factors in this are human reaction time and air resistance. If they get stuck, ask them to drop a pencil and an unfolded sheet of paper. Then have them repeat the experiment, but this time with a pencil and a tightly wadded piece of paper. Ask them why the wadded paper fell faster, and they should see that air resistance slowed the paper the first time.
Answer for Extension Activity
- K = 9.931 x 10-14 s2 m-3
R = 6375 + 600 km = 6.975 x 106 m
Therefore, T = 5805 seconds or 96.7 minutes
- v = 7550 m/sec (about 25 times the speed of sound)
- Astronauts are not really weightless in orbit. In fact, they weigh at least 85% of their weight on Earth. The effect that is usually called "weightlessness" is more correctly called "freefall." The astronauts are falling towards the Earth (moving "vertically") at the same rate as their space vehicle travels "horizontally," so they never actually fall to the Earth. You can experience freefall without leaving the Earth – just try jumping off a diving board or into the air. You will feel "weightless" until you hit the surface of the pool or the ground.
- Most students will predict the heavier object will hit first.
- They should find that the objects hit at the same time.
- This answer will depend on their prediction. Reasons the experiment might be thrown off could be that they didn't let go of the objects simultaneously, that the person viewing the impact didn't see it clearly, or that air resistance slowed one of the objects more than the other.
- Many may change their prediction, saying both will hit simultaneously.
- Most people are surprised that objects with very different masses will fall at the same rate.
- Your teacher has supplied you with a collection of different objects. Look over them: are they all the same size, the same weight?
Pick two of the objects that have different weights and sizes. They should be different enough that you can easily feel the difference. If they are dropped from the same height, will one hit the floor first, or will they hit at the same time?
Make a prediction about this, and record it.
- Now take the objects and hold them in front of you. Make sure the bottoms of the objects are the same height from the floor. Have another student kneel or lie down on the floor in front of you so they have a good view of where the objects will land.
Count backwards from three, and on "zero" drop the objects at the same time. Did one hit first? If so, which one? Note what happened on your worksheet. Repeat the procedure at least twice more to make sure you get consistent results.
- Was your prediction accurate? Why or why not? Can you think of any ways your experiment might have been thrown off? Explain.
- Now find two objects that are roughly the same size, but very different weights. Repeat the experiment, and again record your prediction and the results
- Did the results surprise you? Why or why not?
- My predictions:
- This is what I observed:
- Accurate predictions?
- Observations of second experiment:
- Were you surprised? Why or why not?
- Would you weigh more or less on Mercury than you do on Earth?
- How about Jupiter?
- How much would you weigh on the Moon?
- What is the difference between mass and weight?
- If Swift weighs 1500 kilograms on the surface of the Earth, how much does it weigh at an orbit of 600 km above the Earth's surface?
- You would weigh less on Mercury than on the Earth. (The "g" factor is 0.39 times that of Earth.)
- You would weigh more on Jupiter than on the Earth. (The "g" factor is 2.4 times that of Earth.)
- On the Moon, you would weigh 0.17 times your weight on Earth, or about 1/6 as much.
- Mass is the amount of "stuff" in an object, and weight is the result of the force of gravity acting on that amount of stuff. When you go to a different planet, you look the same (mass) but your weight will change, depending on the changes in the gravitational force.
- The value of "g" in Swift's orbit is 8.2 m/sec2 compared to 9.8 m/sec2 on the surface of the Earth. Swift would therefore weigh 1500 kg x (8.2/9.8) = 1255 kg in orbit.
- NASA Web sites
- NASA's official Web site - http://www.nasa.gov
Swift Satellite - http://swift.gsfc.nasa.gov - NASA Education Resources
- Imagine the Universe! - https://imagine.gsfc.nasa.gov
The Space Place - http://spaceplace.nasa.gov - Check out these videos
- "Liftoff to Learning: Newton in Space" (1992), $15.00
"Flight Testing Newton's Laws" (1999), $24.00 - NASA Resources for Earth and Space Science Education
- NASA Wavelength - http://nasawavelength.org/
- Newton's Laws of Motion
- http://www-istp.gsfc.nasa.gov/stargaze/Snewton.htm
http://www.grc.nasa.gov/WWW/K-12/airplane/newton.html - Newton's Law of Gravitation
- http://csep10.phys.utk.edu/astr161/lect/history/newtongrav.html
- Newton in the Classroom
- http://www.physicsclassroom.com/Class/newtlaws/newtltoc.html
http://www.glenbrook.k12.il.us/gbssci/phys/Class/newtlaws/u2l1a.html - The Nine Planets
- http://nineplanets.org/
Assessment
| Points | Part A: The Fall of Man | Part B: Gravity of the Situation |
| 4 | A) Student is able to predict the motion of objects falling to the ground B) Student is able to make repeatable measurements of falling objects C) Student is able to thoughtfully consider the initial predictions and revise them, if incorrect D) Student is able to correctly conclude that mass has no effect on acceleration | A) Student is able to correctly calculate the accelerations for all the solar system bodies listed in the table B) Student is able to correctly calculate all the ratios of the accelerations with respect to that of Earth C) Student is able to thoughtfully consider the results of the calculations and provide correct answers about Mercury, Jupiter and the Moon D) Student is able to correctly describe the difference between mass and weight |
| 3 | Student achieves the first three objectives above. | Student achieves the first three objectives above. |
| 2 | Student achieves the first two objectives above. | Student achieves the first two objectives above or at least half of the first two objectives and the third objective. |
| 1 | Student achieves only the first objective above. | Student achieves only the first objective above or parts of the first two objectives |
| 0 | Student achieves none of the objectives above. | Student achieves none of the objectives above. |
Answers to In-Class Activity Questions
Part A: The Fall of Man
Part B: The Gravity of the Situation
| Planet or Body Name | Mass (m) |
Radius (kg) |
Acceleration (m/sec2) |
Acceleration compared to Earth (m/sec2) |
| Mercury | 3.3 x 1023 | 2.4 x 106 | 3.8 | 0.39 |
| Venus | 4.9 x 1024 | 6.1 x 106 | 8.9 | 0.90 |
| Earth | 6.0 x 1024 | 6.4 x 106 | 9.8 | 1.0 |
| Moon | 7.4 x 1022 | 1.7 x 106 | 1.7 | 0.17 |
| Mars | 6.4 x 1023 | 3.4 x 106 | 3.7 | 0.38 |
| Jupiter | 1.9 x 1027 | 7.1 x 107 | 23.1 | 2.4 |
| Saturn | 5.7 x 1026 | 6.0 x 107 | 9 | 0.92 |
| Uranus | 8.7 x 1025 | 2.6 x 107 | 9 | 0.91 |
| Neptune | 1.0 x 1026 | 2.5 x 107 | 11 | 1.1 |
| Pluto | 1.3 x 1022 | 1.2 x 106 | 0.60 | 0.062 |
Student Handout
Newton's Law of Gravitation
Name: ________________________
Date: ________________________
Period: ________________________
You already know about gravity: it holds you down to the Earth. But there is more to gravity than that! In this activity you will investigate a few properties of gravity and see how it affects you – not just on Earth, but on other planets!
The goal of Part A is to determine the relationship between the acceleration due to gravity and the mass of an object. The goals of Part B are to determine how much you would weigh on other planets and how that weight is affected by the mass and radius of the planet.
Part A: The Fall of Man
Answer the following (use a separate sheet of paper if necessary)
Part B: The Gravity of the Situation
Newton's model of gravity is one of the most important scientific models in history. It applies to apples falling from trees, baseballs soaring into the outfield, and milk being spilled in your school cafeteria. The exact same model applies to other planets in our Solar System, too!
Use the Solar System table given below to determine the value of g, the acceleration due to gravity, for each of the other planets in the Solar System. Use the equation for acceleration in the box and the values for the masses and radii of the planets listed in the table. Complete the third column of the table with the value for the surface gravitational acceleration for each planet (and the Moon).
g = GM/R2
where M = mass, R = radius,
and G = 6.672 x 10-11 N m2/kg2
Complete the solar system data chart:
| Planet or Body Name | Mass (m) |
Radius (kg) |
Acceleration (m/sec2) |
Acceleration compared to Earth (m/sec2) |
| Mercury | 3.3 x 1023 | 2.4 x 106 | ||
| Venus | 4.9 x 1024 | 6.1 x 106 | ||
| Earth | 6.0 x 1024 | 6.4 x 106 | ||
| Moon | 7.4 x 1022 | 1.7 x 106 | ||
| Mars | 6.4 x 1023 | 3.4 x 106 | ||
| Jupiter | 1.9 x 1027 | 7.1 x 107 | ||
| Saturn | 5.7 x 1026 | 6.0 x 107 | ||
| Uranus | 8.7 x 1025 | 2.6 x 107 | ||
| Neptune | 1.0 x 1026 | 2.5 x 107 | ||
| Pluto | 1.3 x 1022 | 1.2 x 106 |
Once you complete the third column, you can see how strong (or weak) gravity is on other planets. A better way to understand this is to compare the gravity of the planets with the Earth's. So in the last column, divide the gravity you got for the other planets by the Earth's gravity (for example, after you do this, you will get the Earth's gravity = 1, since you are dividing the number you got for Earth's gravity by itself).
Think about it!
Answer the following



