Fermi

Active Galaxy Educator Guide

An Educator's guide with Activities in Science and Mathematics

active galaxy poster

Table of Contents

Active Galaxies and the Fermi Education and Public Outreach Program

Busy educators sometimes have trouble finding ways to help their students feel the excitement of science in action. As a part of its educational effort, the NASA Education and Public Outreach group at Sonoma State University (SSU) has put together a series of activities presentation based on the science of one of NASA's exciting space missions: the Fermi Telescope.

Since many students remember and understand better when they actively engage in manipulating the concepts about which they are learning, we have included several hands-on activities to help keep their interest and reinforce their comprehension and retention of the scientific concepts covered in the presentation of the mission. We have also included information about Fermi, what kind of objects it will observe and why astronomers are interested in them. To help you determine when this project might be of most use to you in your science and/or math curriculum, we have included a matrix of the math and science standards covered. This introduction to the activities includes the answers to some frequently asked questions.

What is Fermi?

The Fermi Telescope is a NASA satellite that was launched in 2008. Fermi is part of NASA's Structure and Evolution of the Universe theme. The astronomical satellites in this theme are designed to explore the structure of the Universe, examine its cycles of matter and energy, and peer into the ultimate limits of gravity: black holes. Fermi detects gamma rays, the highest energy light in the electromagnetic spectrum. Fermi was built in collaboration between NASA, the U.S. Department of Energy, France, Germany, Italy, Japan, and Sweden. The project is managed from NASA's Goddard Space Flight Center in Greenbelt, Maryland.

Where do gamma rays come from?

Gamma ray sources include black holes, pulsars, supernova remnants, and active galaxies. Active galaxies will be a very common source of high-energy gamma rays detected by Fermi. Thousands of these sources will be studied during its mission.

What instruments does Fermi use?

There are two scientific instruments on board Fermi: the Large Area Telescope (LAT) and the Fermi Burst Monitor. The LAT is the primary instrument, and issurveying the sky in high-energy gamma-ray light. It is also studying many individual sources of gamma rays. The Fermi Burst Monitor is detecting Gamma Ray Bursts, tremendous explosions coming from vast distances. These explosions are thought to signal the birth of black holes.

What will my students learn from these activities?

This series of activities uses active galaxies – distant galaxies with supermassive black holes in their cores – as an engagement to teach basic concepts in physical science and mathematics. The mapping of the activities to the relevant national standards is shown by the matrix on page 4, and a more detailed listing of the standards met by each activity can be found in pages 31 through 33.

How are these activities organized?

The Introduction to Active Galaxies section has a general introduction to active galaxies. Depending on the age and ability of your students, you may need to tell them about this information, have them read it, or have a few advanced students put together a presentation to the rest of the class based on this introduction and other sources they may find. With this introduction, try to convey the excitement of the scientists when they first discovered interesting phenomena related to active galaxies, such as the super-massive black holes at their cores, and the high-energy jets of particles that are sometimes emitted.

Each activity has some or all of the following components to help you make it an exciting learning experience for the students:

  1. Science concepts and estimated time. (Note: time varies significantly for different age groups and levels of science understanding.)
  2. Background information specific to this activity. (See the suggestions above for possible ways to present this background information.)
  3. The "essential question" asked by the activity. Take the time to help students understand that scientists ask questions. Each activity states the essential question that this activity is designed to answer, or to help the student explore.
  4. The materials needed to complete the activity.
  5. A list of abbreviations used and possible additional notes to the teacher.
  6. The specific learning objectives of this activity.
  7. The step-by-step procedures to be followed for the most efficient and effective use of the activity.
  8. An assessment rubric for the activity. It is important that before you start an activity you have a clear understanding of what constitutes a successful activity. This assessment rubric suggests ways to evaluate your students' work in mastering the activities' objectives.
  9. Transfer activities: One of our goals in science is to help students see science and scientific concepts as tools to be used throughout their lives, not just as a small part of their education. Including transfer activities after the activity is completed will not only reinforce the specific objectives, but also help your students learn to apply scientific concepts to their "real lives."
  10. Suggested extension and reflection activities. These help the student follow up the activity with comprehension exercises so that they better assimilate the information, and use the concepts they have learned to better understand phenomena in everyday life.
  11. Lesson adaptations that will help you cope with special needs students.
  12. An answer key that provides you with the answers to the questions given to the students, and that will help you evaluate the products the students may produce as a part of this activity.
  13. Student worksheets that contain the information and directions necessary for the student to complete the activities. NOTE: giving the students the work sheet without the appropriate background information and procedures will not only decrease the learning of the students, it may also cause frustration and feelings of inadequacy to master science principles.
  14. Detailed Standards list that explains how each activity meets the specific national science and mathematics standards.
  15. A glossary that briefly defines each term with which the student may be unfamiliar (these appear in bold letters the first time they are used in the activity).
  16. A list defining any acronyms used.
  17. A resource list which will help you find more information about the topics in the activities.

Who developed these activities?

The activities and the poster that describes active galaxies have been developed as part of the NASA Education and Public Outreach (E/PO) Program at Sonoma State University, under the direction of Professor Lynn Cominsky.

Contributors to this education unit also include Dr. Philip Plait, Lynda Williams, Sarah Silva, Michelle Curtis, Aurore Simonnet, Tim Graves, and Dr. Mary Garrett. We would also like to acknowledge input from Kara Granger and Dr. Laura Whitlock to an earlier version of the first activity, and helpful comments from Sharon Janulaw, Teena Della, Christine Royce, Dr. William Keel, Dr. Greg Madejski, Tom Arnold, Rae McEntyre, Bruce Hemp, and Tom Estill.

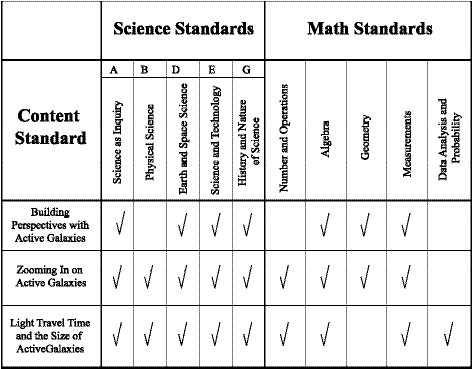
National Content Standards Matrix

The activities in this booklet conform to these national science and mathematics education standards. Detailed standards met by each activity are listed for each activity at the end of this document (Activity 1, Activity 2, and Activity 3).

Standards matrix

Introduction to Active Galaxies

A galaxy is a system of stars, gas, and dust bound together by their mutual gravity. A typical galaxy has billions of stars, and some have trillions. Although they come in many different shapes, the basic structure is the same: a dense core of stars called a 'nucleus' surrounded by stars and gas. Normally, the core of a disk or elliptical galaxy is small, relatively faint, and composed of older, redder stars. However, in some galaxies the core is intensely bright, shining with power equivalent to trillions of suns, easily outshining the rest of the light of the galaxy combined. A galaxy that emits such tremendous amounts of energy is called an active galaxy. Active galaxies are actually rare, but so bright they can be seen clear across the visible universe.

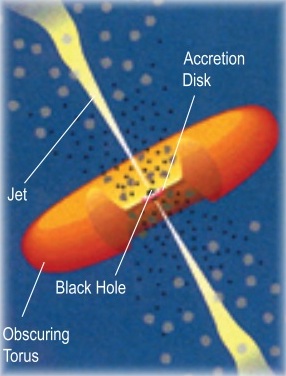
Illustration of an active galactic nulceus and it's various components

Figure 1: An artist's illustration of an active galaxy.

It is believed that at the center of these bright galaxies lies a supermassive black hole millions or even billions of times the mass of our Sun (Figure 1). As matter falls toward the black hole, it forms an accretion disk, a flattened disk of material swirling around the black hole. Friction and magnetic forces inside the disk heat it to millions of degrees, and it glows brightly nearly all the way across the electromagnetic spectrum, from radio waves up to X-rays. Although our own Milky Way Galaxy has a central supermassive black hole, it is not an active galaxy. For reasons currently unknown, the black hole at the center of our Galaxy is quiescent, or inactive, as are most present-day galaxies.

Although the physics underlying the phenomenon is not well-understood, it is known that in some cases the accretion disk focuses long jets of matter which streak away rom the core at speeds near that of light. The jets are highly collimated (meaning they retain their narrow focus over vast distances) and are emitted in a direction perpendicular to the disk. Eventually, they slow to a stop due to friction with gas well outside the galaxy, forming giant clouds of matter that radiate strongly at radio wavelengths (radio lobes; Figure 2). In addition, surrounding the accretion disk is a torus (donut) of molecular material. From certain viewing angles, this torus can obscure observations of the black hole and accretion disk.

There are many types of active galaxies. Initially, when astronomers were first studying them, it was thought that the different types of active galaxies were fundamentally different objects. Now astronomers generally (but not universally) accept the unified model of active galaxies, meaning that most or all active galaxies are actually just different versions of the same object. Many of the apparent differences between types of active galaxies are due to viewing the active galaxy at different orientations with respect to the disk, or due to observing the active galaxy in different wavelengths of light.

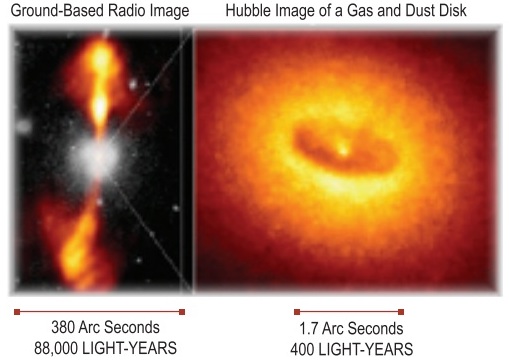
Double-lobed radio galaxy NGC 4261

Figure 2: Double-lobed radio galaxy NGC 4261.

Activity 1: Building Perspectives with Active Galaxies

Science Concepts

  • There are different components in active galaxies.
  • Different viewing angles lead to dramatic differences in the appearance of simple objects.

Essential Question

What do active galaxies look like when viewed from different directions?

Duration

60 minutes

Background Information

The type of active galaxy we see depends on the way that we see it. If we see the accretion disk and gas torus edge on, the galaxy is called a radio galaxy. The torus of cool gas and dust blocks most of the radiation from the inner black hole and its nearby environment, so the most obvious features are the radio emitting jets and giant lobes well outside the galaxy.

If the disk is tipped slightly to our line of sight, we can see higher-energy light from the accretion disk inside the gas torus in addition to the lower energy radio waves. This kind of active galaxy is called a Seyfert galaxy (named after American astronomer Carl Seyfert, who first catalogued these galaxies in 1943). It looks much like a normal galaxy but with a very bright core, and may be giving off high-energy photons like X-rays. If the galaxy is very far away from us, we may see the core as a star-like object even if the fainter surrounding galaxy is undetected. In this case, the galaxy is called a quasar, which is short for quasi-stellar radio source (so-named because the first ones discovered appeared to be star-like through a telescope, but emitted copious radio waves, unlike "normal" stars). The first quasar to be discovered, dubbed 3C273, was found to be a galaxy at a very large distance by astronomer Martin Schmidt in 1963.

If the tip angle is 90 degrees, we can be looking straight down a jet. This type of active galaxy is called a blazar. From blazars we see very high-energy gamma ray photons. The first blazar to be discovered, BL Lac (and after which we get the term "blazar") was found in 1926 to change in brightness, but was thought to be a normal star! It wasn't until the late 1970s that its galactic nature was truly revealed.

In sum, the basic components of an active galaxy are: a supermassive black hole core, an accretion disk surrounding it, and a torus of gas and dust, and in some (but not all!) highly focused jets of matter and energy. The type of active galaxy we see depends on the way we see the galaxy: radio galaxies, Seyferts, quasars and blazars.

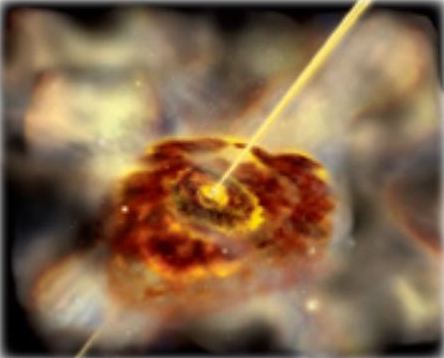
Artist's illustration of an active galaxy

Figure 3: Artist's illustration of an active galaxy.

Materials

For each group of 2 or 3 students:

  • Styrofoam ball (1.5 inch or 4 cm in diameter)
  • 2 toothpicks
  • 1 lightweight sheet of construction paper
  • 1 heavier weight sheet of construction paper
  • 3 pages of blank or bond white paper
  • scissors
  • compass
  • ruler
  • cellophane tape
  • colored pencils or pens

Objective

Students will build a model of an active galaxy. From this, they will learn about the geometry of the components of the galaxy and understand that different viewing angles lead to dramatically different appearances of the galaxies.

Procedure

  1. Introduce the activity by using the information in the Introduction to Active Galaxies and in the activity Background Information above.
  2. Discuss these questions with the students before starting the activity: Do objects look the same from all angles? Are they recognizable from all angles? For example, it's not difficult to recognize a book from almost any viewing angle. But is every object like that? How do we recognize objects if viewed from unfamiliar angles? How do we categorize unfamiliar objects if seen from different angles?
  3. Explain to the students that they will be building a model of an active galaxy from a styrofoam ball, construction paper, toothpicks and tape. This model will help them answer the questions on the worksheet. The model building can be done in groups of two or three.
  4. Have the students make observations of the model, then sketch them as viewed from different angles. This should be done individually.

Assessment

The students' work can be assessed using the following rubric:

  • 4 points:
    • All calculations are correct.
    • Model is assembled correctly and neatly.
    • Drawings are complete and neatly done.
    • Description of different views are correct.
  • 3 points:
    • One calculation is incorrect, or one drawing is drawn/labeled incorrectly, or one description is incorrect.
  • 2 points:
    • Two calculations are incorrect, or two drawings drawn/labeled incorrectly, or model built incorrectly, or two descriptions are incorrect, or some combination.
  • 1 point:
    • Drawings or descriptions are incorrect.
  • 0 points:
    • No work turned in

Extension Activities

Compare and contrast the students' drawings to those on the Fermi Active Galaxies Poster for the different viewing angles. Discuss how this activity changes their perspectives about how they view and interpret what they see in the Universe.

Transfer Activities

Have the students examine and draw everyday objects from different angles. Pass the drawings around to other students and see if they can identify the object, especially if the viewing angle is unfamiliar.

Lesson Adaptations

Visually impaired students may have difficulty constructing the models and drawing them. Put the model in their hands, and let them note by touch how the model feels different if they can only access one part of it at a time (for example, a single cone/jet). They can examine how the model feels different if they keep their hand flat, fingers extended, and can only touch the model that way. In that example, the opening of the cone will feel like a circle, and the torus will feel flat. Have them describe how limiting their ability to touch the model limits their ability to identify its parts.

Answer Key for "Building Perspectives with Active Galaxies"

  1. 1.5 inches or 4 cm
  2. If the conical paper jet is properly constructed, it will obscure the styrofoam ball (black hole).
  3. For a 4 cm diameter styrofoam ball, the minimum width of the strip should be 4 cm (1.5 inches).
  4. If D is the outer diameter of your disk, then the circumference of the torus is πD. For an 8 cm disk, the circumference is then 8π.
  5. This answer will depend on the student. In general, looking straight down the jets will hide the black hole, accretion disk and torus. From an angle, the black hole, accretion, disk and torus will be visible, and the jets will be elongated. The far jet may be difficult to see. From the side, the black hole and accretion disk are again hidden, this time by the torus. Both jets will be visible and about the same size.

Activity 2: Zooming in on Active Galaxies

Science Concepts:

  • The small angle approximation has limits.
  • The angular size of an object depends on its distance and its physical diameter.

Essential Question

What do active galaxies look like when viewed from different distances?

Duration

45 minutes

Background Information

Artist's illustration of an active galaxy from a distance

Figure 4: Artist's illustration of an active galaxy at a great distance.

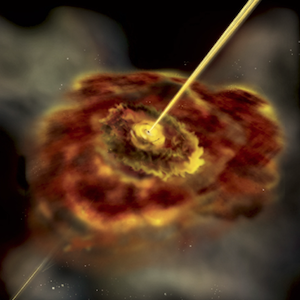
Artist's illustration of zooming in on active galaxy

Figure 5: Artist's illustration of zooming in on active galaxy.

Artist's illustration of zooming in to the central engine of an active galaxy

Figure 6: Artist's illustration of zooming in to the central engine of an active galaxy.

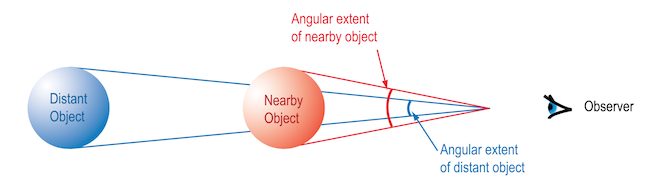
The appearance of a distant object and the amount of detail we can see in it is directly related to how far away it is from us - the closer an object is, the larger it appears and the easier it is to see details; the farther away it is, the smaller it appears and the harder it is to see details. Although active galaxies are often hundreds of thousands of light years in size, their great distances make them challenging to observe in detail. In this activity we explore how the distance to an active galaxy affects how we see it.

Let's imagine distance is not a factor and take a fantasy flight into a cartoon active galaxy that has jets. The long view of the active galaxy is dominated by lobes of radio emission caused by highly focused twin jets of matter streaming out from the galactic nucleus (Figure 4). Closer in, a torus of dust and gas can be seen orbiting outside a flatter disk of gas (Figure 5). In an extreme close-up, the invisible black hole in the center is surrounded by a flat accretion disk of rapidly orbiting material. Jets are emitted at right angles from the plane of the disk, driven by physics still not well understood (Figure 6).

Now let's consider a real active galaxy: the double-lobed radio galaxy NGC 4261, which is located approximately 100 million light years from Earth. The Hubble Space Telescope and ground-based radio images (Figure 1, on page 5) of NGC 4261 shows radio lobes that span some 100,000 light years out from a spiral-shaped disk of gas and dust 400 light years in diameter. Presumably, a small but supermassive black hole "engine" lies at the center of the nucleus with a mass 1.2 billion times the mass of the Sun and contained in a space about the size of the solar system - about 6 billion kilometers. Imagine that!

How much detail can we actually see with the Hubble Space Telescope (HST) in a galaxy 100 million light years away?

The smallest objects HST can discern have an angle of about 0.1 arcseconds (about 0.00005 times the width of the full Moon). Using the small angle approximation this angular diameter translates into a linear size of 460 trillion kilometers at the distance of NGC 4261! This is over 100,000 times larger than the effective size of the black hole. That's why we can't directly see the black hole at the core of the galaxy. Rather, we infer the existence and the properties of the black hole indirectly by observing the effect it has on the gas and stars surrounding it.

The Fermi observatory, designed to detect gamma rays from active galaxies, has a resolution of roughly 0.5 arcminutes (about 1/60th the width of the full Moon). Although no current detection technology exists that can see the central black hole in an active galaxy, Fermi is able to detect gamma rays produced by the jets with unprecedented sensitivity. Such data will help us understand the physical processes that are going on in the nucleus and the supermassive black hole engine that fuels it.

Additional Background

We imagine the sky to look like a giant hollow sphere surrounding the Earth. It really isn't, but real objects are so far away that we have no real perception of distance, and so when we look at stars in the sky our brain interprets them as being infinitely far away. This gives the sky an illusion of being a hollow sphere with us at the center.

When astronomers measure the size of objects in the sky or the distance between them, they use angular size. A circle drawn all the way around the sky is divided into 360 degrees, so two objects on opposite sides of the sky are said to be 180 degrees apart. An object that spans a quarter of the sky's circumference would be 90 degrees across, and so on. The disk of the Moon in these units has an angular diameter of 0.5 degrees. Degrees are further subdivided into 60 arcminutes (the term "arc" is to help distinguish this from a measure of time, and the unit is abbreviated as a single tick mark: ') and each arcminute is further divided into 60 arcseconds (abbreviated with a double tick mark: "). The Moon can thus be described as having an angular diameter of 30 arcminutes, or 1800 arcseconds. Most distant astronomical objects such as galaxies are fractions of an arcsecond to a few arcminutes in angular extent.

The relationship between angular diameter, distance, and appearance is shown below: the closer an object is, the larger the angle it covers and the larger it appears; the farther away an object is, the smaller the angle it covers and the smaller it appears.

Illustration of the small angle approximation

Mathematically, angular diameter, linear diameter, and distance can be combined in an extremely useful and simple equation called the small angle approximation. As seen in the figure below, the angular diameter, α, depends on the distance to the object, D, and its actual linear diameter, d, according to:

tan(α/2) = d/2D

The students will show in this part of the unit, for very small values of α measured in radians, tan(α) = α. Using this approximation, the equation relating distance and linear size simplifies further to

α/2 = d/2D or more simply α = d/D

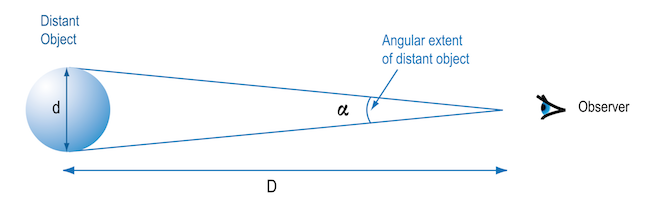
Illustration of the small angle approximation

In the small angle approximation, if any two of the quantities are known, the third can be calculated. In astronomy, the angular diameter is usually measured directly and the equation is used to calculate the distance or the physical diameter of the object. Since distances to astronomical objects are usually much larger than their linear sizes, this approximation is of great use in all branches and at all levels of astronomy!

The following table provides a summary of the unit conversions discussed above, along with some other abbreviations that will be used later in the unit. It may be useful for your students to have access to this table.

Abbreviations

  • α - angular diameter
  • cm - centimeters
  • ° - degrees
  • d - diameter
  • D - distance
  • ly - light year
  • m - meters
  • mm - millimeters
  • % - percentage
  • rad - radian
  • s - second

Conversion Factors

  • Light year to meters: 1 ly = 9.5 x 1015 m
  • meters to centimeters: 1 m = 100 cm
  • Kilometers to meters: 1 km = 1000 m
  • Radians to degrees: 1 rad x 180°/π rads = 57.3°

Note for the teacher: Just like with hands, some people are right-eyed and others left-eyed. The instructions for the template construction below assume the student will be using their right eye. When the students are constructing the template, they can reverse left and right in the directions if they prefer to use their left eye.

Materials

For each group of 3 students:

  • Fermi Active Galaxies Poster
  • protractor
  • stiff cardboard
  • 1 heavier weight sheet of construction paper
  • 3 pages of blank or bond white paper
  • meter stick or tape measure
  • pencil
  • scissors or knife
  • scientific calculator

Objectives

  • Students will be able to accurately use and understand the small angle formula, and demonstrate this by filling out a table.
  • Students will be able to construct a template and use it to correctly measure the angular size of a person.
  • Students will be able to use the Active Galaxies Poster to measure the angular size of a galaxy.

Procedure

  1. Introduce the activity by reviewing the information in the Introduction to Active Galaxies and the activity Background Information.
  2. Discuss these questions with the students: Can they recognize their friend's face from across the room? How about from across a football field? How far away can someone be and still be recognizable?
  3. Explain to the students that they will be doing a series of three activities that will teach them how the angular size of objects changes with distance.
  4. The small angle activity (Part A) should be done individually. The other two activities (Parts B and C) should be done in teams of three people each. Part A can be eliminated if time is not available.
  5. For Part C, "Measuring the Size of a Galaxy Using the Active Galaxy Poster," you will need to affix the poster to a wall, and make sure the students have about 5 meters of clear space between them and the poster. You can mount the poster at the end of a hallway or on the wall of a large classroom.

Assessment

There are three separate activities that comprise this unit. They can be assessed using the common rubric below either individually or as a group.

  • 4 points:
    • All calculations are correct.
  • 3 points:
    • One calculation is incorrect, or off by more than 10%.
  • 2 points:
    • Two calculations are incorrect.
  • 1 point:
    • More than two calculations are incorrect.
  • 0 points:
    • No work turned in

Transfer Activities

Students can test the limits of their vision and measure angles of familiar objects. For example, the width of a finger held at arm's length is typically 1–2 degrees. This can be calibrated by having them mark their angle template in degrees from 1–10, and using it to measure the width of their fingers held at arm's length. By comparing the known size of an object (say, the length of a car) to the width of their finger, they can approximate the distance to the object using the small angle formula.

Extension Activities

Derive the small angle formula more rigorously, following the rules of trigonometry. Given that the Moon is 3500 km in diameter and 0.5° in angular size, have the students calculate the distance to the Moon. Have them look up the correct answer and compare it to their calculated answer.

Reflection Activities

Where else would the small angle formula be useful? Examples: in surveying, hunting, sports, or anywhere else where gauging the distance would be necessary.

Lesson Adaptations

If the student is visually impaired, and cannot measure the angles using the template in Activity 2, s/he can be the person whose height is measured, or can use the meter stick to measure distances. If the student is mobility-impaired, s/he can be the person whose height is measured (Student B).

Answer Key for "Zooming In on Active Galaxies"

Part A:

Angle (degrees) Angle (radians) Tangent (angle) Difference % Difference
0.5000 0.0087 0.0087 0.0000 0.0025
1.000 0.0175 0.0175 0.0000 0.0102
2.000 0.0349 0.0349 0.0000 0.0406
4.000 0.0598 0.0599 0.0000 0.1528
8.000 0.1396 0.1405 0.0009 0.6550
15.00 0.2618 0.2679 0.0058 2.349
20.00 0.3491 0.3640 0.0149 4.270
25.00 0.4353 0.4663 0.0300 6.870
30.00 0.5236 0.5774 0.0538 10.27
35.00 0.6109 0.7002 0.0893 14.63
40.00 0.6981 0.8391 0.1410 20.19
  1. The small angle approximation works well for the full Moon.
  2. Yes, the small angle approximation should work very well.

Part B: Answers for questions 3 through 8 will depend on each student's height. Below is a reference table with distances given the students' height.

Student Height (cm) Distance (cm) for
0.17 radians = 10°		 Distance (km) for
0.0001 radians = 0.5 arcmin
140 802.1 9.626
150 859.4 10.31
160 916.7 11.00
170 974.0 11.69
180 1031 12.38
190 1069 13.08
200 1146 13.75
  1. On average, the typical human eye can see objects about 1/60th of a degree across, so the answer to this question is "no."
  2. 13.0 centimeters. Note the significant figures should reflect 0.1 cm accuracy.
  3. The distance should be 149 cm. This will depend on their measuring accuracy.
  4. This will depend on their distance measurement, but should be close to the actual disk size of 13 cm.
  5. This will depend on their accuracy. They should be within 10% or so of the measured size.
  6. 893.8 meters.
  7. 17.5 centimeters. Note the significant figures should reflect 0.1 cm accuracy.
  8. The distance should be 200.5 cm, and will depend on their measuring accuracy.
  9. This will depend on their distance measurement, but should be close to the actual lobe size of 17.5 cm.
  10. This will depend on their accuracy. They should be within 10% or so of the measured size.
  11. 1203.2 meters.
  12. 446.9 meters.
  13. 1.38 million light years.
  14. 100 million / 1.38 million = 73, so the magnification would be 73X

    15. Activity 3: Light Travel Time and the size of Active Galaxies

    Science Concept

    • The changes in the intensity of a galaxy's light can be used to measure the size of the galaxy.

    Essential Question

    How is the speed of light used to measure the physical sizes of objects that are otherwise too far away to measure directly?

    Duration

    45 minutes

    Background Information

    Active galaxies do not usually emit a steady stream of light. Instead, their brightness can change dramatically over the span of weeks, days and even minutes. Fermi is detecting this variability from thousands of active galaxies with great accuracy. Amazingly, this variability can tell astronomers quite a bit about the active galaxy itself, including its size!

    Illustration of the small angle approximation

    Illustration of an active galaxy emitting a light flash that travels to observer.

    Astronomers can find the size of the active galaxy emitting region using a clever technique. It involves knowing the speed of light, and being able to set limits on how quickly an object can change its brightness.

    Imagine an object that measures one light-week across as in the figure below. Suppose that the entire object emits a brief flash of light. Photons from the part of the object nearest to the Earth arrive at our telescopes first. Photons from the middle of the object arrive at the Earth some time later. Finally, light from the far side of the object arrives after a measurable time difference from the arrival of the first photons. Although the object emitted a sudden flash of light, we observe a gradual increase in brightness that lasts a full week, from the first recorded incident. In other words, the flash is stretched out over a time interval equal to the difference in the light travel time between the nearest and most remote observable regions of the object.

    If an object is 1 light-year in diameter, it will take 1 year longer for the signal from the far side of the object to be detected than the signal from the near side. To calculate the diameter of the emission region from the duration of the brightness variation we multiply the velocity of light (called c which equals 3x 10^8 m/s), by the length of time (called t or "delta t" or Δt) it takes the active galaxy to change brightness. When multiplied together they tell you the size of the emitting region:

    Size of emitting region = (speed of light) x (time of variation)
    or
    Size = c Δ t

    Astronomers refer to this technique as using the light travel time (ct) to find the size of an object.

    Example: A time variation of one week is observed. Determine the diameter of the active galaxy's active region:

    d = (speed of light) x (time of variation)
    = (3 x 108 m/s) x (1 week)

    Since 1 week = 7 days x 24 hrs/day x 3600 sec/hr = 604, 800 seconds

    d = (3 x 108 m/s) x (604,800 seconds)
    d = 1.81 x 1014 m

    The solar system is roughly 1013 meters across, so the active galaxy emitting region in this example is about 18 times the diameter of the solar system - an astoundingly small distance given that a typical active galaxy can have a billion times the mass of our sun and about 1000 times the luminosity of the entire Milky Way galaxy!

    There is a limit to this method. For example, if you only observe an object once a day, you won't see variations shorter than that timescale. Therefore, the smallest region you can measure is 2 light days (about 5 x 1013 meters, or five times the diameter of the solar system) across. The region is 2 light days across because you need to observe the object once, see its brightness rise, then see it fall. That takes three observations; the first, the second a day later, and the third a day after that: a two day interval. So when you measure the size based on brightness variations, it's really an upper limit. There might be smaller scale regions, but you cannot detect them.

    Also, the object may be emitting over various timescales: there may be short duration bursts or flares on top of much longer, slower variations. Generally speaking, astronomers assume that the shortest duration variation is what tells us the size of the emitting region. The speed of light is the maximum speed the variation can travel across the object, but there may be slower methods too. So the quickest variation gives you an upper limit to the size of the region. It may be smaller than the calculated size, but not bigger.

    In this exercise, the student takes data from a graph (see page 26) and uses it to calculate the total energy emitted by a flare every second. The flux from an object is defined as the amount of energy that passes through an area of one square meter every second. In the case of the graph of a flare from 3C279 (see page 26), the plot shows the photon flux, which is the number of gamma-ray photons hitting one square meter every second. The graph is telling us that the flare generated about 5 x 10-2 photons per square meter per second. If we assume that each gamma ray hitting the detector has an energy of 100 million electron Volts (abbreviated 100 MeV; about 100 million times the energy of a visible light photon), the photon flux can be converted to an energy flux.

    That energy flux is the amount of energy hitting a square meter every second here on Earth. The Earth is at a vast distance from 3C279, so we only intersect a tiny fraction of the total energy emitted. If we could put a sphere around 3C279 such that the radius of the sphere is the distance from the Earth to the active galaxy, we would capture all the energy. If you add up all the energy in every square meter of the sphere, you will have the total energy emitted by the flare per second, what astronomers call the luminosity. The students will first find the flux from the graph, then multiply it by the total area of that sphere, yielding the total luminosity of the flare. By dividing by the Sun's luminosity, they can directly compare the energy of the flare to the energy of the Sun. The ratio is huge, meaning that the flare emitted vastly more energy than the Sun does. Finally, they will calculate how long it would take the Sun to emit as much energy as the flare did in one second. The answer may surprise (and humble) you: the flare emitted about 36 trillion times as much energy as the Sun does every second, or the amount of energy emitted by the Sun for over a million years!

    Ask the students to think about that number for a moment. This was a single flare emitted by an object. The ratio they calculated was the energy of the flare in gamma rays only to the total energy of the Sun! In reality, even more energy was emitted by the flare, since the flare also emitted X-rays, ultraviolet, optical light, etc. Ask them if they would want to be anywhere near this object, and comment on what might happen if our own Milky Way Galaxy became an active galaxy.

    Materials for each student

    • calculator
    • pencil

    Objectives

    • Students will be able to use a simple equation to determine the size of a flare emitting region given the rise and decay times.
    • Students will be able to measure the rise and decay times of a flare using a plot with actual NASA data from an active galaxy.
    • Students will be able to compare the total energy emitted by the flare to the energy of the Sun.

    Procedures

    1. Introduce the activity by reviewing information in the Introduction to Active Galaxies and in the activity Background Information.
    2. Discuss the speed of light with the students in terms of the distance covered in a given amount of time. How long would it take a beam of light to cross the Earth? Travel to the Moon? The Sun? The scale of the Universe is a very misunderstood topic; covering this topic before the activity will give the students a better sense of that scale. Ask them if a light year is a unit of distance or time. Many students will say "time," but the light year is a unit of length (equal to 9.5 x 1015 m).
    3. Explain to the students that they will be doing two activities to measure the size and energy of a flaring region in an active galaxy. In the first activity, they will use a simple equation to determine the size of the region given the duration of a flare from that region. In the second they will measure the rise and decay times themselves using a plot with actual NASA data of an active galaxy. From there, they can compare the total energy emitted by the flare to the energy of the Sun.
    4. The activities should be done individually.

    Transfer Activities

    The idea that distance equals (speed x time) can be applied to many situations. For example, a car traveling at 100 kilometers per hour for two hours will travel a total of 200 kilometers. Have the students calculate the distance they can travel in a given time (say, 3 hours) given different vehicles: walking at 5 km/hr, bicycling at 30 km/hr, a car at 100 km/hr, a plane at 1000 km/hr, a satellite at 11 km/sec.

    Extension Activities

    Do we see galaxies as they are "all at once," or do we see some parts before others? A variation on the travel time idea is to use the delay between seeing an object and hearing a noise it makes to determine its distance. Imagine a lightning storm kilometers across, with two simultaneous bolts, one from the near side and the other from the far side. Do we hear the thunder at the same time? (No.) Do we see the bolts at exactly the same time? (No.) Is the delay between the two sounds the same as the delay between the two flashes? (No; the flashes are separated by milliseconds while the thunderclaps are separated by many seconds.) Given the speed of sound (~500 meters/second), have the students determine the distance to a lightning bolt given the delay in hearing the sound. (Each second of delay corresponds to 500 meters of distance.)

    Reflection Activities

    How do dolphins use the differences in travel time in reflected sounds to see around them? Bats? Ask the students to think of where else this technique might be useful (radar, echo mapping of planet surface, distance to lightning storm).

    Assessment

    There are two separate activities that comprise this unit. They can be assessed using the common rubric below either individually or as a group.

    • 4 points:
      • All calculations are correct.
    • 3 points:
      • One calculation is incorrect, or off by more than 10%.
    • 2 points:
      • Two calculations are incorrect.
    • 1 point:
      • More than two calculations are incorrect.
    • 0 points:
      • No work turned in

    Answer Key for "Light Travel Time and the Size of Active Galaxies"

    Part A:

    Time Size (meters) Size (solar system)
    1 hour 1.1 x 1012 0.11
    1 day 2.6 x 1013 2.6
    1 week 1.8 x 1014 18
    1 year 9.5 x 1015 950
    1. 4.7 seconds
    2. 9 days
    3. 2.33 x 1014 meters
    4. 23.3 solar systems
    5. 3 days
    6. 7.8 x 1013 meters
    7. 7.8 solar systems
    8. Since the same region is assumed to be getting brighter and then fading away, whichever time is faster should indicate the size of the region. The slower time indicates a larger region, but this larger region could not change in a shorter time. Therefore the faster time is a better indicator of the size of the region, which for this example is about 7.8 x 1013 meters across. Another way to think about it: imagine the region is actually the size indicated by the slower change. That would mean it was 9 light days across. Would it be able to fade in 3 days? No, assuming it fades all at once, we would still see it as taking 9 days to fade. So it must actually be 3 light days across, and it took longer to rise in brightness due to some other physical effect.

    Part B:

    1. Looking at the points for the minimum and maximum of the flare during its rise:
      Slope = rise/run = (4.5 x 10-2 photon m-2 sec-1 – 1.4 x 10-2 photon m-2 sec-1) / (176.5 days – 167.5 days) = 3.44 x 10-3 photon m-2 sec-1 day-1. To get the y-intercept, set y = mx + b and plug in the x and y for either the maximum or the minimum. The y-intercept is then –5.6 x 10-1 photon m-1 sec-1.
    2. For the decay, rise/run = (4.5 x 10-2 photon m-2 sec-1 – 1.0 x 10-2 photon m-2 sec-1) / (176.5 days – 179.5 days) = -1.17 x 10-2 photon m-2 sec-1 day-1. The y-intercept is 2.1 photon m-2 sec-1.
    3. Add two weeks (14 days) to the time of maximum and put it into the y-intercept formula. x would then be 176.5 + 14 = 190.5, and y = mx + b , so y = 9.32 x 10-2 photon m-2 sec-1.
    4. Since the decay rate is still shorter than the rise time, and the flare size depends on the shorter time, the flare size is still the same as found before.

    Part C:

    1. Maximum flux = (4.5 x 10-2 photon m-2 sec-1)(100 MeV/photon) = 4.5 MeV m-2 sec-1.
    2. Maximum flux = (4.5 MeV m-2 sec-1)(106 eV/MeV) / (6.3 x 1018 eV/J) = 7.14 x 10^-13 J m-2 sec-1.
    3. Area = 4p[(4x109 light years)(9.5 x 1015 m/light year) ]2 = 1.8 x 1052 m2.
    4. Area x flux = (1.8 x 1052 cm2)( 7.14 x 10-13 Joules m-2 sec-1) = 1.3 x 1040 Joules/sec.
    5. (1.3 x 1040 Joules/sec) / (4 x 1026 Joules/sec) = 3.24 x 1013.
    6. 3.24 x 1013 /3 x 107 = 1.08 x 106 years or about 1.1 million years!

    Glossary

    Definitions

    Accretion Disk
    the flattened disk of matter swirling just outside the black hole
    Active Galaxy
    a galaxy with an unusually large amount of energy emitted from the nucleus.
    Angular Size
    the angle between the lines of sight to the two opposite sides of an object.
    Annular
    shaped like or forming a ring.
    Apex
    the point or tip of the cone; a peak.
    Arcminute
    1/60th of a degree.
    Black Hole
    an object so small and dense that inside its event horizon, the escape velocity is faster than the speed of light. In an active galaxy, the central black hole may have millions or even billions of times the Sun's mass.
    Blazar
    a quasar that one is viewing directly down the jet axis.
    Degree
    1/360th of the circumference of a circle.
    Electron Volt (eV)
    a unit of energy commonly used in astronomy. A typical gamma ray has an energy of about 100 million electron Volts (100 MeV).
    Flare
    a sudden, dramatic increase in brightness of an object.
    Flux
    the amount of energy passing through an area of one square meter every second.
    Galaxy
    a collection of gas, dust, and billions of stars.
    Jet
    a thin, highly focused beam of matter and energy emitted from the nuclei of some active galaxies. Jets can be hundreds of thousands of light years long.
    Joule (J)
    a unit of energy, equal to 6.3 x 1018 eV.
    Light-Week
    the distance light travels in a week; approximately 181 billion kilometers (1.8 x 1011 kilometers) or 1.8 x 1014 m.
    Light-Year
    the distance light travels in one year; approximately 10 trillion kilometers (1013 kilometers) or 9.5 x 1013 m.
    Luminosity
    the total energy emitted by an object per second.
    Photon
    an individual quantum or particle of light.
    Quasar
    An active galaxy so distant it appears star-like.
    Quiescent
    at rest; inactive.
    Radian
    1/(2π) of the circumference of a circle. One radian = 57.3 degrees
    Radio galaxy
    a galaxy that is a powerful source of radio waves.
    Radio Lobe
    A large radio-wave emitting cloud of matter located at the ends of the jets in some active galaxies, formed when the matter from the jet is slowed by intergalactic material.
    Seyfert galaxy
    an active galaxy (named for astronomer Carl Seyfert) where the inner disk is tipped to our line-of-sight, allowing us to see higher energy light from the nucleus.
    Solar System
    a collection of planets, moons, comets, etc. which orbits a star. Our solar system is roughly 1010 kilometers (1013 meters) across.
    Torus
    A doughnut-shaped object. Gas and dust outside the accretion disk in an active galaxy orbit the central black hole in a torus-shaped region.

    Acronyms

    E/PO
    Education and Public Outreach
    GLAST
    Gamma-Ray Large Area Space Telescope (former name for Fermi)
    HST
    Hubble Space Telescope
    LAT
    Large Area Telescope (on Fermi)
    NASA
    National Aeronautics and Space Administration
    SSU
    Sonoma State University

    Detailed Standards For Each Activity

    Activity 1: Building Perspectives with Active Galaxies

    National Science Education Standards
    • Content Standard A: Science as Inquiry
      • Abilities necessary to do scientific inquiry

        Students investigate their model of an active galaxy and compare/contrast it with images of real galaxies using logic and evidence from real and constructed models. Reflection and transfer activities give the students the opportunity to extrapolate what they have learned to everyday experiences.

      • Understandings about scientific inquiry

        Results of scientific inquiry: by examining the model active galaxy, the students will be able to grasp why scientists developed the unified model of active galaxies, and why there are so many different types of active galaxies.

    • Content Standard D: Earth and Space Science
      • Origin and Evolution of the Universe

        Galaxies are a fundamental structure in the Universe, and the supermassive black holes in their nuclei are in turn a fundamental part of galaxies. This activity strengthens students' understanding of the structure of galaxies.

    • Content Standard E: Science and Technology
      • Understandings about science and technology

        Students see that in order to understand the wide range of astronomical objects they must use different techniques to observe them. Students should understand that looking at the objects isn't enough; scientists must use their imagination to understand objects they cannot see.

    • Content Standard G: History and Nature of Science
      • Science as a human endeavor

        Students will understand the initial confusion of scientists about active galaxy types, and how scientists were able to make progress in understanding them.

    NCTM - Mathematics Standards
    • Algebra
      • Use mathematical models to represent and understand quantitative relationships

        The model of the active galaxy is constructed by using measurements and analyzed to see the relationship to the real object in space.

    • Geometry
      • Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships

        Students observe the finished models and create illustrations to show how two-dimensional representations of a three-dimensional object can change under rotation.

      • Apply transformations and use symmetry to analyze mathematical situations

        Students examine the symmetry of the active galaxy model at different aspect angles.

      • Use visualization, spatial reasoning, and geometric modeling to solve problems

        Students use their constructed active galaxy to analyze and illustrate its appearance at different angles. The geometry of the model is critical to understanding the relationships of the different active galaxies.

    • Measurements
      • Understand measurable attributes of objects and the units, systems, and processes of measurement

        The construction of the model involves measurements to create the components. The properties (size, shape, etc.) of the actual active galaxy cores are compared to the models. The students make decisions about units and scales.

      • Apply appropriate techniques, tools and formulas to determine measurements

        The construction of the active galaxy model involves formulae to determine, for example, the size of the torus. The students answer questions about the size and shape of the various model components.

      • Use representations to model and interpret physical, social and mathematical phenomena

        Students construct active galaxy models and compare/contrast them with images of real galaxies.

    Activity 2: Zooming In on Active Galaxies

    National Science Education Standards
    • Content Standard A: Science as Inquiry
      • Abilities necessary to do scientific inquiry

        Students make calculations to test the small angle formula (hypothesis and observation). Using their own calculations, the students formulate and revise the theory about an object's size. After having analyzed measurements of nearby objects, students answer questions that engage thought and analysis about real objects in space.

      • Understanding about scientific inquiry

        Students learn how scientists determine the distance and/or size of an object in space.

    • Content Standard B: Physical Science
      • Motion and Forces

        Jets of materials are ejected at velocities near light speed from the black hole in an active galaxy. Students answer questions to help them see how big the jets from active galaxys are, and how we can see them at vast distances.

    • Content Standard D: Earth and Space Science
      • Origin and Evolution of the Universe

        Active galaxies are a fundamental part of the evolutionary process of the universe.

    • Content Standard E: Science and Technology
      • Understanding about science and technology

        The small angle formula is an essential tool used by astronomers to get physical dimensions of astronomical objects.

    • Content Standard G: History and Nature of Science
      • Science as a human endeavor

        Students answer questions about the ability of the human eye to distinguish objects, showing how this activity affects them in daily life. Students see that by working in groups they can formulate better hypotheses about scientific inquiries due to the extra input from others.

    NCTM - Mathematics Standards
    • Numbers and Operations
      • Compute fluently and make reasonable estimates

        Students calculate the accuracy of the small angle formula and complete a table of these values. Students compute sizes and distances of teammates, drawings on the poster and actual astronomical objects. They estimate limits of the human eye's resolution.

    • Algebra
      • Represent and analyze mathematical situations and structures using algebraic symbols

        The small angle formula uses algebra to determine the distance and size of objects.

      • Use mathematical models to represent and understand quantitative relationships

        Students determine the relationship between size and distance, measure these properties in teammates and compare these measurements to active galaxies.

    • Geometry
      • Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships

        Students measure the apparent two-dimensional diameter of three-dimensional objects (teammates), and see how this changes with distance.

      • Use visualization, spatial reasoning, and geometric modeling to solve problems

        Students investigate two- and three-dimensional objects and see the relationship of the size of the object relative to themselves.

    • Measurements
      • Understand measurable attributes of objects and the units, systems, and processes of measurement

        Students measure themselves and drawings on a poster using various units, and compare them to astronomical distances and sizes.

      • Apply appropriate techniques, tools and formulas to determine measurements

        Students use the small angle formula and measurements of each other to gather information about the physical characteristics of objects. Percent difference (error margin) is also used.

    Activity 3: Light Travel Time and the Size of Active Galaxies

    National Science Education Standards
    • Content Standard A: Science as Inquiry
      • Abilities necessary to do scientific inquiry

        Using astronomical data similar to that used by professionals, the students investigate light seen from an active galaxy. Students must formulate and revise scientific explanations based on the series of questions being asked of them.

      • Understanding about scientific inquiry

        Students see that scientists analyze scientific data in plots to find valuable information about the objects being researched.

    • Content Standard B: Physical Science
      • Interactions of Energy and Matter

        Active galaxies are a huge source of energy. Students map this energy and use it to determine the physical size of the region emitting the energy. The amount of energy in gamma rays emitted by an active galaxy is compared to the total energy emitted by the Sun across the entire electromagnetic spectrum to show that an active galaxy is a much larger source of energy.

    • Content Standard D: Earth and Space Science
      • Origin and Evolution of the Universe

        Active galaxies are a fundamental part of the evolutionary process of the Universe.

    • Content Standard E: Science and Technology
      • Understanding about science and technology

        Students learn a method of analysis that scientists commonly use to investigate properties of astronomical objects. Students learn that a simple graph can reveal a large amount of information about an active galaxy.

    • Content Standard G: History and Nature of Science
      • Science as a human endeavor

        Students do a field study (analyzing real data) as a scientist does.

    NCTM - Mathematics Standards
    • Numbers and Operations
      • Compute fluently and make reasonable estimates

        Students determine numbers from a graph, convert units, and calculate various quantities such as surface area, total energy emitted from a flare, and timescales of phenomena.

    • Algebra
      • Understand patterns, relations, and functions

        Students analyze a plot, calculate the rate of change in the plot, and extrapolate from the data.

      • Represent and analyze mathematical situations and structures using algebraic symbols

        Students determine the point-slope equation of a line, extrapolate the data, and use it to determine physical characteristics of an active galaxy.

      • Analyze change in various contexts

        Students interpret rates of change of the luminosity of an active galaxy using graphical data.

    • Measurements
      • Apply appropriate techniques, tools, and formulas to determine measurements

        Students analyze the data and the error in their measurements. Students determine the equation of a line from a graph, extrapolate that data, and use the extrapolated data to determine physical characteristics of active galaxies.

    • Data Analysis and Probability
      • Develop and evaluate inferences and predictions that are based on data

        Students calculate the luminosity of an active galaxy flare by extrapolating from the given data.

    Resources

    For more information on Fermi and active galaxies, see the Fermi Education and Public Outreach web site:
    https://imagine.gsfc.nasa.gov/educators/programs/fermi/

    This educational unit can be found on the Fermi Education and Public Outreach web site at:
    https://imagine.gsfc.nasa.gov/educators/programs/fermi/classroom/

    The Center for Astrophysical Research in Antarctica has an interesting web page with small angle formula activities:
    http://astro.uchicago.edu/cara/outreach/resources/ysi94/smallangle.html

    Bill Keel's Active Galaxies page:
    http://www.astr.ua.edu/keel/agn/

    Active Galaxies from University of Maryland:
    http://www.astro.umd.edu/resources/introastro/actgal.html

    Ted Bunn's Black Hole tutorial:
    http://cosmology.berkeley.edu/Education/BHfaq.html

    Compton Gamma-Ray Observatory and EGRET:
    http://heasarc.gsfc.nasa.gov/docs/cgro/index.html

    Fermi Project Site at Goddard Space Flight Center. This is the official site for Fermi Project Management at NASA's Goddard Space Flight Center:
    https://fermi.gsfc.nasa.gov/

    Fermi Large Area Telescope (LAT) Collaboration. The Fermi LAT is being managed by personnel at Stanford University. This is the official site for the LAT experiment:
    http://www-glast.stanford.edu/

    Fermi Burst Monitor is being managed by personnel at NASA's Marshall Space Flight Center. This is the official site for the Fermi Burst Monitor experiment:
    http://gammaray.msfc.nasa.gov/gbm/


A service of the High Energy Astrophysics Science Archive Research Center (HEASARC), Dr. Andy Ptak (Director), within the Astrophysics Science Division (ASD) at NASA/GSFC