National Aeronautics and Space Administration

Activity #6a
Modeling Mass in the Solar System and a Galaxy

Part A: Create a mass model of the solar system.

1. Using the chart below, answer the following questions.
   

   1. If the mass of the Sun is represented by 4.55 kg of kitty litter, how much kitty litter would represent the mass of Jupiter?
   2. Of Saturn?
   3. Of Uranus or Neptune?
   4. All the other planets (Mercury, Venus, Earth, Mars, Pluto) combined?

   Object	Mass (kg)	Kitty Litter Equivalent (g)	Avg. Distance from Sun (km)	Mass Inside Orbit (g)
   Sun	2.00 x 1030	4550	0
   Mercury	3.30 x 1023		57.9 x 106
   Venus	4.87 x 1024		108.2 x 106
   Earth	5.97 x 1024		149.6 x 106
   Mars	7.35 x 1022		227.9 x 106
   Jupiter	1.90 x 1027		778.4 x 106
   Saturn	5.69 x 1026		1427 x 106
   Uranus	8.68 x 1025		2871 x 106
   Neptune	1.02 x 1026		4498 x 106
   Pluto	1.3 x 1022		5906 x 106

2. Measure out these masses from the kitty litter for each of the gas planets and for the combination of the terrestrial planets.

3. Optional - Pour out the rest of the kitty litter to represent the mass of the Sun.

4. If you were a space alien entering the solar system, as you approach the Sun you would pass the orbits of the planets. As you passed by the orbits of each of the planets, how much mass (using the "kitty litter equivalents") is left within the distance between you and the Sun? Fill in this information in the fourth column of the chart. Make a graph of this mass vs. distance.

Part B: Create a mass model of a galaxy.

1. Examine a picture of the Andromeda galaxy. Where do you expect the matter to be in the galaxy?

   ____________________________________________________

   ____________________________________________________

   Distribute the kitty litter according to where you expect the matter to be.

2. 

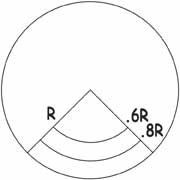
   Select a pie section of your model galaxy. Divide that pie section radially into thirds (so there's an inner portion, a middle portion, and an outer portion). Each third should have the same area. (If R is the radius of the pie section, the first third should extend 0.6R from the center, and the second portion between 0.6R and 0.8R from the center.) If you divide a slice of a galaxy into equal thirds in this manner, would you expect to have the same amount of mass in each? Why or Why not?

   ____________________________________________________

   ____________________________________________________

   ____________________________________________________

   ____________________________________________________

   ____________________________________________________

   ____________________________________________________

3. Determine and record the mass of each third of the slice.
   Outer Third: __________ Middle Third: __________ Inner Third: __________

4. Now imagine you are traveling to the Andromeda galaxy. As you travel through the galaxy, how much mass remains between you and the center? Create a graph of mass vs distance for this.

   ____________________________________________________

   ____________________________________________________

5. Now your teacher will distribute a new material in your galaxy.

6. Determine the mass of each of your portions in the pie section again.
   Outer Third: __________ Middle Third: __________ Inner Third: __________

   Compare with your previous measurements. What do you notice?

   ____________________________________________________

   ____________________________________________________

7. Repeat your imaginary trip through the galaxy. Now what does the graph of mass vs distance look like? If you could see the hidden mass, what do you think the galaxy would look like? Draw a picture of what you think the galaxy would look like if you could see the whole galaxy.

   ____________________________________________________

   ____________________________________________________

   ____________________________________________________