Gamma-Ray Bursts - Apparantly, They Are Absolutely Bright
IV. Activities
1. Apparently, They Are Absolutely Bright
At a press conference discussing the event GRB 990123, Dr. Chryssa Kouveliotou of Universities Space Research Association at the Marshall Space Flight Center said "If the burst had occurred somewhere in our galactic neighborhood, it would have been so bright that night would've turned into day." What exactly does this tell us about how bright it was?
Astronomers express the brightness of stars in visible light in two related forms. Apparent visible magnitude, mv, measures the light that reaches us on Earth. This measure, however, is not a true measure of brightness because distance makes things appear dimmer and apparent magnitude does not correct for this effect. Absolute magnitude, Mv, is a true measure of how much light an object is actually producing. Determining how bright the star (or galaxy or any other emitter) would be if it were located 32.6 light-years (10 parsecs) away compensates for the effect of distance. Note that here we assume space is completely transparent in all directions, so only distance affects what we detect. If clouds of dust intervene between the emitter and us (as they usually do), we have to compensate for that effect too!
Electromagnetic radiation (regardless of whether it is in the form of radio waves, infrared, or gamma-rays) has a common property called the inverse square law. This law states that the amount of energy that is measured by a given detector put at a given distance from an emitter is proportional to the inverse square of the distance from the emitter to the detector. Think about it this way. An emitter E is sitting a distance R away from a detector D. The emitter is radiating equally in all directions. Place an imaginary sphere of radius R around the emitter. The emitter releases a certain amount of energy in 1 second. This energy travels outward in all directions such that in a time T, it reaches the surface of the imaginary sphere a distance R away. This means that now, the original energy, let us call this amount O, is spread out equally over the surface of a sphere of radius R. The surface area of a sphere of radius R is equal to 4 pi R2. Thus, the amount of energy passing through each square centimeter of the sphere is O/4piR2, if R is measured in centimeters. We see, then, that the amount of energy passing through a unit area decreases with the square of the distance from the source. This is the inverse square law of light propagation.
It is important to realize that we now have something to consider when we analyze our observations of the Universe: an object may appear bright because it really is, or it may be bright because it is close by. Conversely, an object may appear dim because it really is, or else it could be just very far away. Such thinking played an important role in the history of understanding GRBs. When they were first detected and their enormous energies calculated, it was believed that they had to be located in our Galaxy. The amount of energy they would be required to produce if they were very far away was just too difficult to seriously consider. Now, however, we know that in fact they are at cosmological distances - that is, very far away indeed. Scientists are still working hard to understand how the enormous energy required for us to be able to detect them from so far away (with the energy falling off as 1/R2) is created. Beaming, which means the energy is not emitted equally in all directions, but instead in a narrowly defined, preferred direction is the most probable answer.
It is easy to demonstrate the fall off of light in your classroom with a graphing calculator, Calculator-Based Laboratory (CBL‘), and light probe. In the exercise, you will measure the intensity (or brightness) of a light as it is moved away from the light probe of the CBL. The resulting data can be graphed and analyzed. For detailed discussions of an activity of this type, see
Real-World Math with the CBL‘ System, Activity 7, Light at a Distance
Exploring Physics and Math with the CBL‘ System, Activity 43, Intensity of Light
Physical Science with CBL‘, Experiment 25, How Bright is the Light?
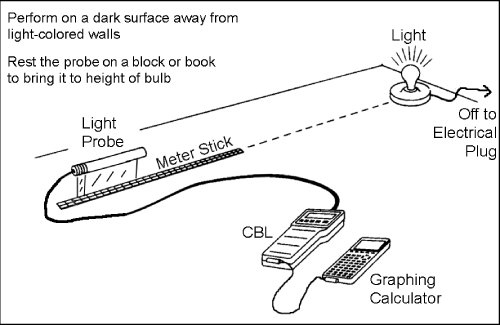
In short, place a 40W (or less) bulb in a shadeless lamp or socket. Put a meter stick at a known distance about 2 meters away from the bulb and on the same level. Place the light probe next to the end of the meter stick closest to the bulb. Make sure nothing obstructs the path between the two. Darken the room. Run the appropriate program on the TI-83 (either BULB, LIGHT, or PHYSCI) and follow the directions it gives you. Make a measurement, then move the probe such that the distance to the bulb increases about 10 cm. Repeat until you have 10 measurements. Plot the intensity values you measured as a function of distance.
• What form do your data take? Linear? Power Law? Quadratic?
______________________________________________________
• Now fit your data using your graphing calculator. What happens to the shape of the line if the fitting parameters become larger? Smaller?
______________________________________________________
Perform the experiment again with either a brighter or dimmer bulb. Consider also taking data at different distances. You should now be able to discuss the following:
• When an astronomer measures the brightness of an object in the Universe, what sort of conclusions can be made about the energy being emitted by that object? What additional information would help the astronomer?
______________________________________________________
______________________________________________________
______________________________________________________
______________________________________________________
______________________________________________________
______________________________________________________
Extensions:
• Investigate the magnitude scale in depth -- learn about Norman R. Pogson; learn about the mathematical equation that relates the magnitude values and fluxes of different objects; learn about where our Sun ranks on the magnitude scale.
• Investigate what astronomers call the distance modulus and use it to determine how bright a star would be on the magnitude scale as you move it closer or further away from Earth. What effects would intervening dust have on this calculation?




