Supernova Chemistry Lesson Plan

How Far? How Powerful?
Keck Spectrum: the Power of GRB 980703
Name: __________________________________
Date: ______
Class: _______________________
Summary
Your teacher has introduced Hubble's Law to you, showing you how you can determine the distance to a galaxy using the redshift of its spectral lines. Using this, and the 1/r2 fall-off of light you previously confirmed, you will calculate the power of a distant gamma-ray burst.
Background
Gamma-ray bursts were discovered in 1969, which is fairly recent in terms of astronomy. (For comparison, we've known about planets since humans first looked the sky!) Gamma-ray bursts, or GRBs for short, last for only a few moments, but in that time they outshine the rest of the gamma-ray sky. They appear in random directions on the sky, and for the past several decades, they have been known as the great mystery of the Space Age.
The first problem astronomers needed to tackle in order to solve the mystery of gamma-ray bursts was to determine where in the sky they were coming from. This was made difficult by the fact that gamma-rays are had to focus, so for many years there was great uncertainty in the positions of GRBs. Finding an optical counterpart to a GRB was like looking for a needle in a haystack. That all changed in the late 1990s.

An artist's impression of the Swift satellite. (Credit: Spectrum Astro)
On December 14, 1997, the BeppoSAX satellite measured the first 'afterglow' of a GRB, ushering in a new era of discovery of these powerful events. On July 3, 1998, astronomers at the Keck Telescope in Hawaii measured the optical afterglow of a GRB that contained many sharp spectral lines. You will use this spectrum to determine the redshift of this object. From its redshift, and our understanding of the expansion of the universe you will measure the distance to this GRB, and ultimately the power of this explosion.
After this first BeppoSAX observation, astronomers began to unravel the mystery of GRBs. The Swift satellite was designed to rapidly repoint during the onset of a GRB to capture the optical and X-ray light of these objects. In its years in orbit, Swift has locked down the nature of GRBs. You can ask your teacher for further resources to see what Swift found!
Procedure
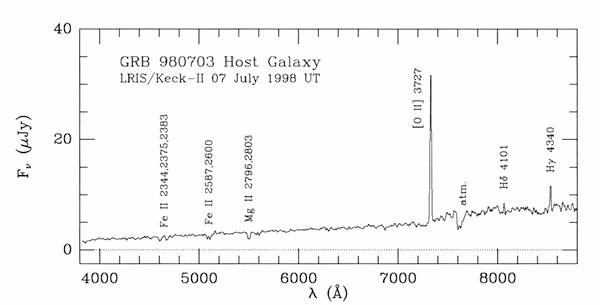
The Keck II telescope on the peak of Mauna Kea in Hawaii was able to observe the spectrum of the glowing remains of a gamma-ray burst just before it faded from our view forever. Below is the spectrum of visible light taken by Keck II of that burst on July 3, 1998.
In the plot, the flux is shown as a function of wavelength. The flux is measured in micro-Janskys (mJy) and the wavelength is measured in angstroms. The plot shows a smooth energy distribution with several emission lines. These lines come from atomic transitions of elements in astronomical sources. Their relative spacing is determined only by the atom that gives rise to the line. The lines marked Hδ and Hγ are due to neutral hydrogen. O II is from ionized oxygen. The 'rest' wavelengths at which these transitions occur in the lab are marked on the plot. The shift in the wavelength from the rest wavelength is due to the motion of the galaxy away from us. This is called Doppler shift.
Use the plot to complete the following steps:
- Using any straightedge, measure the wavelengths of the sharp Hδ, Hγ and O II lines in the spectrum, and record these in the data table.
- Calculate the difference, λ - λ0 and the redshift (λ - λ0)/λ0 and fill those in on the data table.
- Calculate the average redshift of the three lines.
- Use the formula for Doppler shift and the average redshift you calculated to find the velocity of the galaxy away from us. Show your work, and remember to include the correct units.
- Now, use Hubble's Law to find the distance to the galaxy hosting GRB 080703, using the velocity you calculated. Show your work, and remember to include the correct units.
- Convert that distance to light years, km, and cm.
Note: 1 Mpc = 3.26 × 106 light year
1 light year = 9.5 × 1012 km
1 km = 105 cm - Finally, use the 1/r2 fall-off of light to determine the energy of the light emitted from GRB 980703.
| Spectral Line |
Rest Wavelength λ0 (Å) |
Measured Wavelength λ (Å) |
Difference λ - λ0 (Å) |
Redshift (λ - λ0)λ0 |
| O II | 3727 | |||
| Hδ | 4101 | |||
| Hγ | 4340 |
Doppler shift formula:
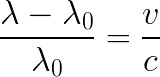
c is the speed of light = 3 × 105 km/sec
Hubble's law:
H0 is the Hubble constant = 70 km/sec/Mpc
Flux emitted:
where the measured flux was 5.27 × 10-6 erg /cm2
Questions to answer
- Compare your distance to GRB 980703 to other
distances. Here are some suggestions (these are given to 2
significant figures, your answers should have the same number of
significant digits), though your teacher may direct you to use other
comparisons or come up with your own:
- Diameter of the Earth: 13,000 km
- Distance to the nearest star (named Proxima Centauri): 4.20 light years
- Distance to nearby galaxy, Andromeda: 2.5 × 106 light years
- Power is defined as the amount of energy exerted over time. GRB 980703 lasted about 300 seconds. Using this and the energy of GRB 980703 that you calculated to determine the power of GRB 980703. Convert your answer from ergs/second to Watts (1 W = 10-7 erg/second).
- Compare the power emitted by GRB 980703 with some other sources.
- Watts in a household lightbulb
- Energy output of the Sun (4 × 1026 Watts)
- Your calculations were all based on the assumption that the gamma-ray burst emits light "isotropically", or in all directions equally. However, astronomers have found that when a gamma-ray burst explodes, the light is actually "beamed", so that most of the light is emitted in two beams of light, as depicted below. Describe how this would change the amount of energy emitted by the GRB. Would your calculation be an over-estimate? An under-estimate? And why?