The Life Cycles of Stars
The Life Cycles of Stars
I. Star Birth and Life
Imagine an enormous cloud of gas and dust many light-years across. Gravity, as it always does, tries to pull the materials together. A few grains of dust collect a few more, then a few more, then more still. Eventually, enough gas and dust has been collected into a giant ball that, at the center of the ball, the temperature (from all the gas and dust bumping into each other under the great pressure of the surrounding material) reaches 15 million degrees or so. A wondrous event occurs.... nuclear fusion begins and the ball of gas and dust starts to glow. A new star has begun its life in our Universe.
So what is this magical thing called "nuclear fusion" and why does it start happening inside the ball of gas and dust? It happens like this..... As the contraction of the gas and dust progresses and the temperature reaches 15 million degrees or so, the pressure at the center of the ball becomes enormous. The electrons are stripped off of their parent atoms, creating a plasma. The contraction continues and the nuclei in the plasma start moving faster and faster. Eventually, they approach each other so fast that they overcome the electrical repulsion that exists between their protons. The nuclei crash into each other so hard that they stick together, or fuse. In doing so, they give off a great deal of energy. This energy from fusion pours out from the core, setting up an outward pressure in the gas around it that balances the inward pull of gravity. When the released energy reaches the outer layers of the ball of gas and dust, it moves off into space in the form of electromagnetic radiation. The ball, now a star, begins to shine.
New stars come in a variety of sizes and colors. They range from blue to red, from less than half the size of our Sun to over 20 times the Sun�s size. It all depends on how much gas and dust is collected during the star�s formation. The color of the star depends on the surface temperature of the star. And its temperature depends, again, on how much gas and dust were accumulated during formation. The more mass a star starts out with, the brighter and hotter it will be. For a star, everything depends on its mass.
Throughout their lives, stars fight the inward pull of the force of gravity. It is only the outward pressure created by the nuclear reactions pushing away from the star's core that keeps the star "intact". But these nuclear reactions require fuel, in particular hydrogen. Eventually the supply of hydrogen runs out and the star begins its demise.
II. Beginning of the End
After millions to billions of years, depending on their initial masses, stars run out of their main fuel - hydrogen. Once the ready supply of hydrogen in the core is gone, nuclear processes occurring there cease. Without the outward pressure generated from these reactions to counteract the force of gravity, the outer layers of the star begin to collapse inward toward the core. Just as during formation, when the material contracts, the temperature and pressure increase. This newly generated heat temporarily counteracts the force of gravity, and the outer layers of the star are now pushed outward. The star expands to larger than it ever was during its lifetime -- a few to about a hundred times bigger. The star has become a red giant.
What happens next in the life of a star depends on its initial mass. Whether it was a "massive" star (some 5 or more times the mass of our Sun) or whether it was a "low or medium mass" star (about 0.4 to 3.4 times the mass of our Sun), the next steps after the red giant phase are very, very different.
III. The End
A. The Fate of Sun-Sized Stars: Black Dwarfs
Once a medium size star (such as our Sun) has reached the red giant phase, its outer layers continue to expand, the core contracts inward, and helium atoms in the core fuse together to form carbon. This fusion releases energy and the star gets a temporary reprieve. However, in a Sun-sized star, this process might only take a few minutes! The atomic structure of carbon is too strong to be further compressed by the mass of the surrounding material. The core is stabilized and the end is near.
The star will now begin to shed its outer layers as a diffuse cloud called a planetary nebula. Eventually, only about 20% of the star�s initial mass remains and the star spends the rest of its days cooling and shrinking until it is only a few thousand miles in diameter. It has become a white dwarf. White dwarfs are stable because the inward pull of gravity is balanced by the electrons in the core of the star repulsing each other. With no fuel left to burn, the hot star radiates its remaining heat into the coldness of space for many billions of years. In the end, it will just sit in space as a cold dark mass sometimes referred to as a black dwarf.
B. The Fate of Massive Stars: Supernovae! and Then...
Fate has something very different, and very dramatic, in store for stars which are some 5 or more times as massive as our Sun. After the outer layers of the star have swollen into a red supergiant (i.e., a very big red giant), the core begins to yield to gravity and starts to shrink. As it shrinks, it grows hotter and denser, and a new series of nuclear reactions begin to occur, temporarily halting the collapse of the core. However, when the core becomes essentially just iron, it has nothing left to fuse (because of iron's nuclear structure, it does not permit its atoms to fuse into heavier elements) and fusion ceases. In less than a second, the star begins the final phase of its gravitational collapse. The core temperature rises to over 100 billion degrees as the iron atoms are crushed together. The repulsive force between the nuclei overcomes the force of gravity, and the core recoils out from the heart of the star in an explosive shock wave. As the shock encounters material in the star's outer layers, the material is heated, fusing to form new elements and radioactive isotopes. In one of the most spectacular events in the Universe, the shock propels the material away from the star in a tremendous explosion called a supernova. The material spews off into interstellar space -- perhaps to collide with other cosmic debris and form new stars, perhaps to form planets and moons, perhaps to act as the seeds for an infinite variety of living things.
So what, if anything, remains of the core of the original star? Unlike in smaller stars, where the core becomes essentially all carbon and stable, the intense pressure inside the supergiant causes the electrons to be forced inside of (or combined with) the protons, forming neutrons. In fact, the whole core of the star becomes nothing but a dense ball of neutrons. It is possible that this core will remain intact after the supernova, and be called a neutron star. However, if the original star was very massive (say 15 or more times the mass of our Sun), even the neutrons will not be able to survive the core collapse and a black hole will form!
IV. More about the Stellar Endpoints
A. White/Black Dwarfs
A star like our Sun will become a white dwarf when it has exhausted its nuclear fuel. Near the end of its nuclear burning stage, such a star expels most of its outer material (creating a planetary nebula) until only the hot (T > 100,000 K) core remains, which then settles down to become a young white dwarf. A typical white dwarf is half as massive as the Sun, yet only slightly bigger than the Earth. This makes white dwarfs one of the densest forms of matter, surpassed only by neutron stars.
White dwarfs have no way to keep themselves hot (unless they accrete matter from other closeby stars); therefore, they cool down over the course of many billions of years. Eventually, such stars cool completely and become black dwarfs. Black dwarfs do not radiate at all.
Many nearby, young white dwarfs have been detected as sources of soft X-rays (i.e. lower-energy X-rays); soft X-ray and extreme ultraviolet observations enable astronomers to study the composition and structure of the thin atmospheres of these stars.
B. Neutron Stars
Neutron stars are typically about ten miles in diameter, have about 1.4 times the mass of our Sun, and spin very rapidly (one revolution takes mere seconds!). Neutron stars are fascinating because they are the densest objects known. Due to its small size and high density, a neutron star possesses a surface gravitational field about 300,000 times that of Earth.
Neutron stars also have very intense magnetic fields - about 1,000,000,000,000 times stronger than Earth's. Neutron stars may "pulse" due to electrons accelerated near the magnetic poles, which are not aligned with the rotation axis of the star. These electrons travel outward from the neutron star, until they reach the point at which they would be forced to travel faster than the speed of light in order to still co-rotate with the star. At this radius, the electrons must stop, and they release some of their kinetic energy in the form of X-rays and gamma-rays. External viewers see these pulses of radiation whenever the magnetic pole is visible. The pulses come at the same rate as the rotation of the neutron star, and thus, appear periodic. Neutron stars which emit such pulses are called pulsars.
C. Black Holes
Black holes are objects so dense that not even light can escape their gravity and, since nothing can travel faster than light, nothing can escape from inside a black hole. Nevertheless, there is now a great deal of observational evidence for the existence of two types of black holes: those with masses of a typical star (4-15 times the mass of our Sun), and those with masses of a typical galaxy. This evidence comes not from seeing the black holes directly, but by observing the behavior of stars and other material near them!
Galaxy-mass black holes are found in Active Galactic Nuclei (AGN). They are thought to have the mass of about 10 to 100 billion Suns! The mass of one of these supermassive black holes has recently been measured using radio astronomy. X-ray observations of iron in the accretion disks may actually be showing the effects of massive black holes as well.
The Electromagnetic Spectrum as a Probe of the Universe
All objects in our Universe emit, reflect, and absorb electromagnetic radiation in their own distinctive ways. The way an object does this provides it special characteristics which scientists can use to probe an object�s composition, temperature, density, age, motion, distance, and other chemical and physical characteristics. Astronomers can time events (for instance, recording exactly when a binary star system is eclipsed and for how long), can obtain the energy distribution of a source (by passing its electromagnetic radiation through a prism or grating to break it into component colors), or can record the appearance of a source (such as taking an image of the source). These three methods are by no means exclusive of each other, but each reveals different aspects of a source and each method gives the astronomer slightly different information.
While the night sky has always served as a source of wonder and mystery, it has only been in the past few decades that we have had the tools to look at the Universe over the entire electromagnetic (EM) spectrum and see it in all of its glory. Once we were able to use space-based instruments to examine infrared, ultraviolet, X-ray, and gamma-ray emissions, we found objects that were otherwise invisible to us (e.g., black holes and neutron stars). A "view from space" is critical since radiation in these ranges cannot penetrate the Earth's atmosphere. Many objects in the heavens "light up" with wavelengths too short or too long for the human eye to see, and most objects can only be fully understood by combining observations of behavior and appearance in different regions of the EM spectrum.
We can think of electromagnetic radiation in several different ways:
- From a physical science standpoint, all electromagnetic radiation can be thought of as originating from the motions of atomic particles. Gamma-rays occur when atomic nuclei are split or fused. X-rays occur when an electron orbiting close to an atomic nucleus is pushed outward with such force that it escapes the atom; ultraviolet, when an electron is jolted from a near to a far orbit; and visible and infrared, when electrons are jolted a few orbits out. Photons in these three energy ranges (X-ray, UV, and optical) are emitted as one of the outer shell electrons loses enough energy to fall down to the replace the electron missing from the inner shell. Radio waves are generated by any electron movement; even the stream of electrons (electric current) in a common household wire creates radio waves ...albeit with wavelengths of hundreds of kilometers and very weak in amplitude.
- Electromagnetic radiation can be described in terms of a stream of
photons (massless packets of energy), each traveling in a wave-like
pattern, moving at the speed of light. The only difference between radio
waves, visible light, and gamma-rays is the amount of energy in the
photons. Radio waves have photons with low energies, microwaves have a
little more energy than radio waves, infrared has still more, then
visible, ultraviolet, X-rays, and gamma-rays. By the equation
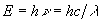, energy dictates a photon�s wavelength and frequency.
Activities
Hey, Low Mass Star....This is your life!
This model shows the discrete stages that a low mass star goes through over billions of years, from its beginnings as a gas cloud, to its death as a black dwarf.
Materials:
* tape
* tissue paper and cotton batting
* string of indoor Christmas lights with white, red, orange, and yellow bulbs
* different-sized spherical light globes either clear or white (ranging from 1 to 5 inches in
diameter; these can be found in any store selling light fixtures)
* opaque black ball (or you could paint a light globe)
Procedure:
1. Punch 6 holes in a piece of cardboard or cotton batting and insert one of the lights through each hole. You might need to tape them in place.
2. To show the birth of a star as a hot gas cloud, wrap the outside of a globe in cotton and place it over the first bulb of the string of lights.
3. For a newborn star, have an orange light inside a 3-inch globe.
4. For a steady star, have a yellow light inside a 2-inch globe.
5. For a red giant, have a red light inside a 5-inch globe.
6. For a planetary nebula, have a red light inside a 3-inch globe. Wrap crumpled tissue paper around the outside of the globe.
7. For a white dwarf, have a white light inside a 1-inch globe.
8. For a black dwarf, have a 1 inch black opaque globe. No lights should be used for the black dwarf.
The globes used for the various stages are not to scale. Do a simple calculation to see why...if a steady star is 1.4 million km in diameter (and represented by a 2-inch globe), how big would the red giant globe have to be on the same scale? You might need to refer back to the information in Section II to help you.
Model a Black Hole
This demonstration allows for a visual depiction of the effect of a large mass on the fabric of spacetime. In particular, what effect a black hole does or does not have on the other stars around it and how that effect depends on the mass of the black hole.
Materials:
* large latex balloon cut open and pulled flat, or sheet of latex
* round bowl, 4"- 5" in diameter
* tape
* package of small round beads
* 1" solid ball bearing (the eraser end of a pencil can be used as a replacement)
Procedure:
1. Tape the sheet of latex (this represents space-time) tightly across the top of some round object...such as a bowl. The sheet should not be so tight that it will tear if stretched further, but should be taut enough that there are not any wrinkles!
2. Scatter a few beads on the sheet of latex (this represents matter that is near the black hole).
Make sure they are spread out to all parts of the sheet.
3. Gently drop the ball bearing onto the sheet of latex (this represents the black hole). Try not to let it bounce! If you don�t have a ball bearing, gently push down on the center of the sheet with the eraser end of a pencil.
4. Explain what happened to the matter when the black hole was put into place. Why did this occur?
5. What would happen if the ball bearing was heavier (or if you push harder on the pencil)? What physical analogy to the black hole may be made?
These Stars are Classified
Annie Jump Cannon (1863 - 1941) was known as the world�s expert in the classification of stars. Her work laid the foundation for modern stellar spectroscopy.
Annie Jump Cannon entered Wellesley College in Massachusetts in 1880 to study astronomy. She became interested in stellar spectroscopy, the process of breaking light from stars down into its component colors so the various elements can be identified. After suffering from scarlet fever, which left her hearing impaired, she earned her master�s degree and then continued her studies at Radcliffe College. She became an assistant at the Harvard College Observatory, the first observatory to include women as staff members. During her career, she observed, classified, and analyzed the spectra of some five hundred thousand stars, assigning each one its place in the sequence O, B, A, F, G, K, and M. In 1911 she almost became a faculty member at Harvard but the university officials refused to promote a woman to such high status. So she became the curator of astronomical photographs, earning a salary of twelve hundred dollars a year. Finally, in 1936, Harvard hired her as a permanent faculty member. She was seventy-three years old at the time.
Astronomers now realize that everything which appears to distinguish one star from another - temperature, luminosity, size, life span -- is determined almost entirely by one factor: the star�s mass. The main sequence along the HR diagram is not a singular evolutionary path, as many had thought, but a portrait of the sky at one moment in time of stars with varying masses.
Below is a version of the Hertzsprung-Russell diagram, which shows how the size, color, luminosity, spectral class, and absolute magnitude of stars relate. Each dot on this diagram represents a star in the sky whose absolute magnitude and spectral class have been determined. Notice that the data appear to clump naturally into groups: main-sequence stars, giants, supergiants, and white dwarfs.
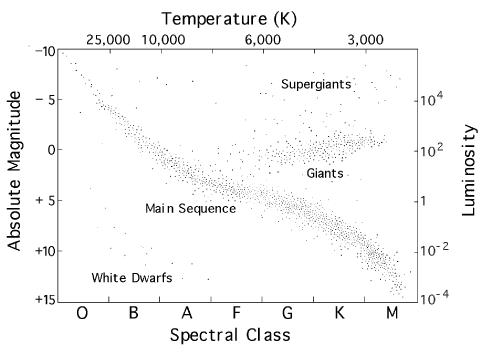
1. Imagine that you are an astronomer and you have detected a source that has a temperature of about 3700 Kelvin, and a luminosity of about 0.1. Examine the H-R diagram; explain what luminosity class and type of source this could be. In what part of its life cycle is this source?
2. What if a source has a temperature of about 10,000 Kelvin, and a luminosity of about 10-3. Explain what type of source this could be, and the part of its life cycle the source is enduring.
3. Make a line plot superimposed on the H-R diagram that would trace the entire life cycle of our star, the Sun. Remember all of the stages of this main-sequence, low mass star.
4. What will be the final stage of evolution (black dwarf, neutron star, or black hole) for each of the following: (Hint: reread the text in Sections I, II, and III)
(a) Type O main sequence star
(b) Type A main sequence star
(c) Type G main sequence star
Suggested Extension:
Examine the difference between absolute magnitude and apparent magnitude. Why is an understanding of this crucial to an astronomer�s ability to describe the evolution of any given star?
Blackbody Radiation & Wien�s Law
A star is considered to be an example of a "perfect radiator and perfect absorber" called a black body. This is an idealized body that absorbs all electromagnetic energy incident on it. A black body is black only in the sense that it is absolutely opaque at all wavelengths; it need not look black. Its temperature depends only on the total amount of radiant energy striking it each second. Stars are good approximations to a black body because their hot gases are very opaque, that is, the stellar material is a very good absorber of radiation.
The energy emitted by black bodies was studied by the German physicist Max Planck. He derived an equation that gives the radiant energy emitted per second from 1 cm2 of a black body�s surface. This equation is called Planck�s Radiation Law and can be written as
.
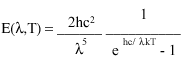In this equation, T is the temperature in Kelvins,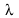 
the wavelength in centimeters,
c the speed of light, k is Boltzmann�s constant (1.37 x
10-18 erg/K), and h is Planck�s constant (6.626 x
10-27 erg sec). Calculus students can prove to themselves that
for such a function there will be a single wavelength, 
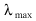, at which maximum light is emitted.
In fact, we can determine that for wavelength in cm and temperature in
Kelvins,
.
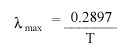This is known as Wien�s Law. This Law is very important to astronomers. It tells us that the wavelength at which a star emits its maximum light indicates the star�s temperature.
1. What are the spectral classes of stars that have the following maximum light wavelengths?
You will need to refer to the H-R Diagram!
(a) 3 x 10-5 cm (b) 1.5 x 10-5 cm (c) 5.5 x 10-5 cm (d) 1.25 x 10-4 cm
2. In what region of the electromagnetic spectrum would objects with the following temperatures be best observed by a scientist�s experiment?
(a) .001 K (b) 800 K (c) 15,000 K (d) 1,750,000 K
Suggested Extension:
Are there really objects in space that have a temperature of 0.001 K? What are you detecting at that temperature?
Bigger than a Breadbox?
The Universe is a very big place and it contains some very big objects. In many images scientists create from data, it is difficult to understand the actual sizes of the objects. In this activity, we want to understand the extent (or size) of some supernova remnants. We will do this by applying a simple physics equation.
In physics, we know that velocity = distance traveled / time it takes to travel that distance.
or 
For this activity, we know that the distance (d) traveled is equivalent to the distance from the initial or central star of the supernova remnant, to the edge of the outer material of the remnant. In addition, we know the velocity (v) at which the material of each remnant is expanding outward, and understand that as the remnant gets older the velocity slowly decreases. Lastly, we know how long ago (t) the initial star blew up in a supernova explosion.
Use this information, and the following data to determine the biggest supernova remnant among those listed below. Be careful with the dimensional analysis!
Data:
Cygnus Expansion Velocity = 1,450 km/sec Age = 20,000 years
Crab Expansion Velocity = 1,500 km/sec Age = 943 years
Tycho Expansion Velocity = 5,200 km/sec Age = 425 years
SN1006 Expansion Velocity = 3,000 km/sec Age = 990 years
Now let us look at things from a different angle. What if you knew that a certain supernova is located about 3 kiloparsecs from Earth. When astronomers look at the remnant with their telescopes, they measure it to be 8 arc minutes (480 arc seconds) in diameter. What is the radius of the remnant in kilometers? Scientists have also measured the expansion velocity to be 4,800 km/sec. In what year did the supernova occur? Perhaps you can look up in a library, or on the World Wide Web, information about supernovae observed to occur in that year and find the common name of this supernova remnant. Need a hint?... Johannes Kepler was a famous astronomer.
A Teaspoon of Starstuff
Subrahmanyan Chandrasekhar (1910-1995) was born in Lahore, a part of India that is now in Pakistan. He won a Government of India scholarship and entered Cambridge University in England to work on his doctorate. As he sailed from India to England, he thought a lot about the death of stars. Using Einstein�s theory of relativity, he calculated that stars of a certain mass should not become white dwarfs when they died; he believed that they should keep on collapsing. He put aside this work, earned his doctorate in 1934, and only later actively returned to his theory. He calculated that stars with more than 1.44 times the mass of the Sun (now known as the Chandrasekhar limit) would not become white dwarfs, but would be crushed by their own gravity into either a neutron star or a black hole. His work was viciously criticized by Sir Arthur Eddington, then the leading authority on stellar evolution and someone greatly admired by Chandrasekhar. His standing diminished by Eddington�s attacks, he came to the United States and was hired to teach at the University of Chicago. There he continued his research, which produced significant advances in the field of energy transfer in stellar atmospheres. Eventually, his calculations about white dwarfs were proven correct. With the recognition of the Chandrasekhar limit, the theoretical foundation for understanding the lives of stars was complete. He won the Nobel Prize in physics in 1983.
There are indeed distinct differences in the states of matter contained in main sequence stars, white dwarfs, and neutron stars. The following exercise will help you to understand just how different they are!
Look at the following chart and use the information you find there to calculate how much a teaspoonful of each object would weigh here on Earth. Assume that a teaspoon will hold about 1.5 cubic-centimeters of material.
Object Mass (grams) Radius (cm)
Sun 1.989 x 10 33 6.96 x 1010
White Dwarf 1 x 10 33 5 x 10 8
Neutron Star 2 x 10 33 9 x 10 5
Can you now relate these numbers to materials you know here on Earth? How much does a teaspoon of water weigh? Or air? Or iron?
Crossing the Event Horizon
If a black hole has no size, how do scientists talk about its surface? Well, we don�t really mean the physical surface of the black hole -- we mean the surface around the black hole at which the escape velocity is equal to the speed of light. In other words, if you are closer to the black hole than the distance to this surface, you cannot escape. If you are further away from the black hole than this distance, then there is still hope for you! The surface is called the event horizon, and its radius is the Schwarzschild radius. (Named for Karl Schwarzschild, an astronomer who was a member of the German army in World War I and died of illness on the Russian front in 1916. He applied the equations of general relativity to see what would happen to light near such a massive object.) It is important to keep in mind that the event horizon is not a physical boundary, but for all intents and purposes is the surface of the black hole. Once inside it, you are cut off from the rest of the Universe forever.
The relationship of the Schwarzschild radius to the black hole mass is simple:
This can be easily understood by looking at the equation for the
escape velocity from any spherical body such as a planet or star,
namely,
, where M and
R are the mass and radius of spherical object. For a black hole,
the escape velocity is equal to c, the speed of light.
- What would be the radius of a black hole with the mass of the planet Jupiter?
- How would the period of the Earth�s revolution change if the Sun suddenly collapsed into a black hole? Note that this can never happen!
- Suppose the Earth were collapsed to the size of a golf ball...becoming a small black hole. What would be the revolution period of the Moon, at a distance of 381,500 km? Of a spacecraft that had been hovering 300 m above a point on the surface of the Earth before its collapse? Of a fly orbiting at 0.5 cm?
About the Poster...
The images on the poster are a combination of actual images and artist�s alterations. The low mass star, low mass red giant, white dwarf, black dwarf, neutron star, and black hole images are all artist�s renditions. The neutron star is depicted to emphasize its powerful magnetic field. The black hole image shows the large accretion disk and jets surrounding the black hole, which cannot be seen. Actual images are described below.
SNR: Einstein IPC image of the Cygnus Loop Supernova Remnant
This image is a color version of Fig. 1 of a paper by W.H. Ku et al. In 1984, Astrophysical Journal, Vol. 278, p. 615-618 who give a detailed discussion of the interpretation (as well as a scale and orientation). The remnant is about 2.5 degrees across. In this image, North is up and East is to the right. Most other images of this remnant are flipped horizontally, so East is on the left.
Betelgeuse: HST image of Betelgeuse
The first direct picture of the surface of a star other than the Sun. Credit: A. Dupree (CfA), R. Gilliland (STScI), NASA (Note: The image has been slightly modified by overlaying a gradient, so it's not quite in its original form.)
Nebula: HST image of Orion Nebula
The Orion Nebula star-birth region is 1,500 light-years away, in the direction of the constellation Orion the Hunter. The image was taken on 29 December 1993 with the HST's Wide Field and Planetary Camera 2. Credit: C.R. O'Dell/Rice University, NASA
Solutions
Hey, Low Mass Star...This is Your Life!
If done to scale, the red giant light globe would be over 5 meters in diameter!
Model a Black Hole
The heavy object representing the black hole will distort the latex surface (representing spacetime) and cause the small objects on the surface to be pulled in toward it... but not if you are too far away. A heavier ball bearing, however, would affect beads further out in the latex sheet...just as a more massive black hole creates a larger distortion in spacetime, thus affecting objects further away.
These Stars are Classified
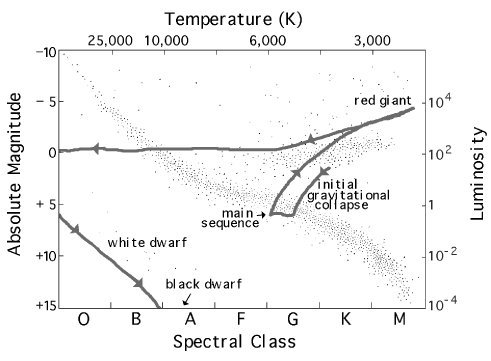
Note that when it goes off this graph on the left side, it actually goes out to about T ~ 100,000 K or higher before turning and heading steadily down to the white dwarf stage.
- (a) black hole; (b) neutron star; (c) black dwarf
Blackbody Radiation and Wien�s Law
1. Solve Wien�s Law for T, substitute in the values for wavelength. With the temperature you obtain, look on the H-R diagram for the corresponding spectral class.
(a) 9656 K Class A; (b) 19,313 K Class B; (c) 5267.2 K Class G; (d) 2317 K Class M
2. Substitute the temperatures into Wien�s Law and obtain the wavelengths of the peak emission. Look up on a chart of the EM spectrum which region the wavelength falls into.
(a) 289.7 cm radio; (b) 3.62x10-4 cm infrared; (c) 1.93x10-5 cm ultraviolet;
(d) 1.65x10-7 cm X-ray
Extension:
No astronomical objects are as cold as 0.001 Kelvin. The radio emission we observe is produced by electrons moving in magnetic fields (this is called synchrotron radiation).
Bigger than a Breadbox?
Using the equation: distance = velocity x time,
Cygnus: 9.14x1014 km; Crab: 4.46x1013 km; Tycho: 6.96x1013 km; SN1006: 9.37x1013 km
The supernova occurred in the year 1604 and is known as Kepler�s supernova. It was observed and documented by the astronomer Johannes Kepler.
A Teaspoonful of Starstuff
Using the equation: mass = density x volume,
We are given that the volume of interest is 1.5 cm3. So what is the density of each of the objects? Density equals mass/volume, and the volume of a sphere is 4/3 p r3, where r is the radius of the sphere. Plugging in the values for each of the types of stars, we find that our teaspoon of the Sun would contain 2.1 grams; of the white dwarf would contain 2.85x106 grams; of the neutron star would contain 9.75x1014 grams. By looking up the density of water, air, and iron, you can calculate that each would be 1,500 grams, 1.935 grams, and 1.179x104 grams, respectively.
Crossing the Event Horizon
1. Using the Schwarzschild equation, we input the mass of Jupiter (1.9x1027 kg), the Gravitational constant (G = 6.67x10-11 m3/kg-sec) and the velocity of light (3x108 m/sec) to see that the event horizon of a Jupiter-mass black hole would occur at 2.96 meters.
2. It would not change.
3. (a) The lunar orbit would take the same as it does now, ~ 27.3 days. The orbit of a spacecraft that had been hovering just over the surface of the Earth would be the same as the current rotation period of Earth, 24 hours. The fly would be inside of the event horizon...so we have no idea what is happening to it!
Glossary
Absolute Magnitude - apparent magnitude a star would have if placed at a distance of 10 parsecs from Earth
Accretion - gradual accumulation of mass
Accretion Disk - a disk of material falling in toward a massive object such as a neutron star or black hole (the disk shape is the result of conservation of angular momentum)
Active Galactic Nuclei - galaxies whose central regions are emitting enormous amounts of electromagnetic radiation
Apparent Magnitude - a measure of observed light flux received from an object at the Earth
Arc Minutes - a unit of measurement used for very small angles; there are 60 arc minutes in one degree
Arc Seconds - a unit of measurement used for very small angles; there are 60 arc seconds in one arc minute
Black Dwarf - the presumed final state of evolution of a low mass star in which no radiation is emitted
Black Hole - region in space where the escape velocity is equal to, or greater than, the speed of light. Thus, nothing (including radiation) can escape from it
Electrical Repulsion - the force which acts between particles of like electrical charge to repel them from each other
Electromagnetic Radiation - radiation consisting of periodically varying electric and magnetic fields that vibrate perpendicular to each other and travel through space at the speed of light
Electromagnetic Spectrum - the full range of electromagnetic radiation spread out by wavelength, it consists of gamma-rays, X-rays, ultraviolet rays, optical light, infrared radiation, microwaves, and radio waves
Electron - a negatively charged subatomic particle that normally moves about the nucleus of an atom
Escape Velocity - minimum velocity an object must achieve to break free from the gravity of another body (in physics, it is achieved when the object�s kinetic energy is equal to its gravitational potential energy)
Event Horizon (also known as Schwarzschild Radius) - the virtual surface around a black hole (often considered as the surface of the black hole) within which gravitational forces prevent anything, including light, from escaping
Expansion Velocity - the outward material velocity away from the central point of an explosion, such as a supernova
General Relativity - the geometric theory of gravitation developed by Albert Einstein, incorporating and extending the theory of special relativity to accelerated frames of reference and introducing the principle that gravitational and inertial forces are equivalent
Gravitational Energy - energy that can be released by the gravitational collapse of a system
Hertzsprung-Russell Diagram - a plot of absolute magnitude versus spectral type (or temperature) for a group of stars
Isotope - any of two or more forms of the same element, whose atoms all have the same number of protons but different numbers of neutrons
Kinetic Energy - energy associated with motion; the kinetic energy of an object is equal to one-half the product of its mass and the square of its velocity
Light-Year - the distance light travels in one Earth year, equal to 9.46 x 1012 km
Luminosity - the rate of radiation of electromagnetic energy into space by a star or other object
Main-Sequence - diagonal region of the Hertzsprung-Russell diagram in which most stars are located; generally these are stable stars during the bulk of their lives
Neutron - a subatomic particle with no electrical charge; one of the constituents of the atomic nucleus
Neutron Star - a star of extremely high density composed almost entirely of neutrons
Nuclear Reaction - a reaction, as in fission, fusion, or radioactive decay, that alters the energy, composition, or structure of an atomic nucleus
Parsec - unit of distance often used by astronomers, equal to 3.2616 light-years (a kiloparsec is equal to 1,000 parsecs)
Photon - a unit of electromagnetic energy associated with a specific wavelength or frequency
Planetary Nebula - a shell of gas ejected from, and expanding away from, a star that is nearing the end of its life
Plasma - a hot ionized gas, that is, it is composed of a mix of free electrons and free atomic nuclei
Potential Energy - stored energy that can be converted into other forms; especially gravitational energy
Proton - a subatomic particle that carries a positive charge, one of the constituents of the atomic nucleus
Radioactive Isotope - an isotope of any element which decays (or decomposes) through the spontaneous emission of subatomic particles and gamma-rays
Red Giant - a star that has greatly increased in size and has a relatively cool surface which glows red; such stars occupy the upper right hand corner of the Hertzsprung-Russell diagram
Resolution - degree to which fine details in an image can be resolved, or separated
Schwarzschild Radius - see Event Horizon
Spacetime - a system of three spatial coordinates and one temporal coordinate with respect to which the time and location of any event can be specified
Special Relativity - the physical theory of space and time developed by Albert Einstein, based on the postulates that all the laws of physics are equally valid in all frames of reference moving at a uniform velocity and that the speed of light from a uniformly moving source is always the same, regardless of how fast or slow the source or its observer is moving
Spectral Class - a classification of a star according to the characteristics of its spectrum
Spectrum - array of colors or wavelengths obtained when light is dispersed, as in passing it through a prism or grating
Star - a self-luminous sphere of gas
Stellar Spectroscopy - breaking down the electromagnetic radiation from a star in order to study the different wavelengths individually
Supergiant - an old, high-mass star greatly expanded from its original size; larger and brighter than a giant star
Supernova - catastrophic explosion of a star which can cause it to shine brighter than a galaxy for a few weeks or so
Supernova Remnant - expanding cloud of radioactive material formed when the outer layers of an exploding star (supernova) are blasted away
White Dwarf - a star that has exhausted most or all of its nuclear fuel, collapsed into a size similar to the Earth; such a star is near the final stage of its evolution
Resources
Books-
Apfel, Necia, Nebulae: The Birth and Death of Stars, 1988, Lothrop, Lee and Shepard, ISBN 0-688-07229-1. Explains the life cycle of stars to upper elementary school students and above.
Branley, Franklyn, Journey Into A Black Hole, 1986, Crowell, ISBN 0-690-04544-1. Explains the black hole stage of a massive star's life cycle to elementary school students and above.
Branley, Franklyn, Superstar: The Supernova of 1987, 1990, HarperCollins, ISBN 0-690-04839-4. Explains the supernova stage of a massive star's life cycle to middle school students and above.
Levy, David H., A Nature Company Guide: Skywatching, 1995, Time-Life Books. This book provides a general overview and discussion of astronomical objects, including the life cycle of stars. For students in middle school or above.
Mitton, Jacqueline & Simon, The Young Oxford Book of Astronomy, 1995, Oxford University Press, Inc. This excellent book explains many concepts in astronomy from the Solar System to galaxies and the Universe, including a nice section on the life cycle of stars. Intended for the middle or high school student.
Magazines-
Berstein, Jeremy, "The Reluctant Father of Black Holes", Scientific American, June 1996, vol. 274, no. 6. Discusses the details of how Einstein's equations of gravity are the foundation of the modern view of black holes. Intended for the high school (and above) student who is interested in science.
Kirshner, Robert P., "SN 1987A: The First Ten Years", Sky and Telescope, February 1997, vol. 93, no. 2. Discussion of the supernova that has taught us much about stellar evolution. Intended for the high school (and above) student who is interested in science.
Hurst, Guy M., "Searching for Outbursts", Astronomy Now, September 1995, vol. 9, no. 10. Talks about how amateur astronomers can help in the search for supernovae. Intended for the high school (and above) student interested in science.
Web sites-
To get a colorful step-by-step overview of the life cycle of stars, examine the site "The Life Cycle of Stars" which is located on the World Wide Web. The URL for this site is
http://astron.berkeley.edu/~bmendez/ay10/cycle/cycle.html
For further information on the various stages of the life cycle of stars, examine the site "Imagine the Universe!" which is located on the World Wide Web. The URL for this site is http://imagine.gsfc.nasa.gov/
Video-
"Evolution of a Star", Starfinder Series #11, Maryland Instructional Technology, 1990. This video can be ordered from the CORE catalog**, or recorded from your local PBS station. It describes the birth, life and death of low mass and massive stars. Intended for the middle school (and above) student.
**Educators may request a catalog and order form by sending a request on school letterhead to the following address:
NASA CORE
Lorain County JVS
15181 Route 58 South
Oberlin, OH 44074
216/774-1051 Ext. 293 or 294
(Mon-Fri) 8-4:00 p.m. E.S.T.
FAX 216/774-2144
Slide Set-
ASP Slide Set #AS238, Stellar Evolution by Dr. James Kaler, 27 slides with captions, $32.95, 1-800-962-3412.
