Life Cycles of Stars (Grades 9-12) - Page 9
2. What if a source has a temperature of about 10,000 Kelvin, and a luminosity of about 10-3. Explain what type of source this could be, and the part of its life cycle the source is enduring.
3. Make a line plot superimposed on the H-R diagram that would trace the entire life cycle of our star, the Sun. Remember all of the stages of this main-sequence, low mass star.
4. What will be the final stage of evolution (black dwarf, neutron star, or black hole) for each of the following: (Hint: reread the text in Sections I, II, and III)
(a) Type O main sequence star
(b) Type A main sequence star
(c) Type G main sequence star
Suggested Extension:
Examine the difference between absolute magnitude and apparent magnitude. Why is an understanding of this crucial to an astronomer�s ability to describe the evolution of any given star?
Blackbody Radiation & Wien's Law
A star is considered to be an example of a "perfect radiator and perfect absorber" called a black body. This is an idealized body that absorbs all electromagnetic energy incident on it. A black body is black only in the sense that it is absolutely opaque at all wavelengths; it need not look black. Its temperature depends only on the total amount of radiant energy striking it each second. Stars are good approximations to a black body because their hot gases are very opaque, that is, the stellar material is a very good absorber of radiation.
The energy emitted by black bodies was studied by the German physicist Max Planck. He derived an equation that gives the radiant energy emitted per second from 1 cm2 of a black body's surface. This equation is called Planck�s Radiation Law and can be written as
.
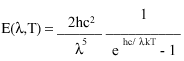In this equation, T is the temperature in Kelvins,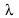 
the wavelength in centimeters,
c the speed of light, k is Boltzmann�s constant (1.37 x
10-18 erg/K), and h is Planck�s constant (6.626 x
10-27 erg sec). Calculus students can prove to themselves that
for such a function there will be a single wavelength, 
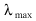, at which maximum light is emitted.
In fact, we can determine that for wavelength in cm and temperature in
Kelvins,
.
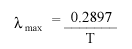This is known as Wien's Law. This Law is very important to astronomers. It tells us that the wavelength at which a star emits its maximum light indicates the star's temperature.
