
The Local Group
About the Image
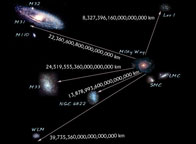
The image of the Local Group is a composite of real images of the actual galaxies that are in the Local Group. The galaxies have been placed in approximately correct orientation, if not scale. The Local Group was first recognized by Edwin Hubble, in the time of the first distance determinations and redshift measurements.

One of the most prominent members of the Local group is M31, the Andromeda Galaxy. It has two small satellite galaxies, M32 and M110.
Also prominent in the local group is the Triangulum Galaxy (M33), Leo I, and NGC 6822. There are over 30 galaxies that are considered to be in the local group, and they are spread over a diameter of nearly 10 million light years, with the center of them being somewhere between the Milky Way and M31. M31 and the Milky Way are the most massive members of the Local Group, with M33 being the 3rd largest. Both M31 and the Milky Way have dwarf galaxies associated with them.
The dynamics of the Local Group are changing, and some astronomers speculated that one day the two large spirals in it (M31 and the Milky Way) may collide and merge to form a giant elliptical galaxy. It is also possible that the Local Group may one day merge with the next nearest big galaxy cluster, the Virgo Cluster.
Distance Information
When we talk about the distances to other galaxies, we often use the units of kiloparsec (kpc) and Megaparsec (Mpc). M31, which is relatively close by, is about 22,360,000,000,000,000,000 km away. This translates to 2.3 million light years, or 725 kpc.
How Do We Calculate Distances of This Magnitude?
Cepheid Variable stars are used to calculate distances of this magnitude. Edwin Hubble used just such a star in the Andromeda Galaxy to find that the galaxy was more than a million light years away - much further than the most distant reaches of our own galaxy.
For more information about Cepheids, please read the section on calculating distances in the Milky Way.
Other methods that are used to find the distances to galaxies can be found on the ABCs of Distance.
Why Are These Distances Important To Astronomers?
We can actually study individual objects (ie a specific star) in Local Group galaxies, even at distances as great as 2,000,000 parsecs. But even with the sharp vision of the Hubble Space Telescope, this can't be done much beyond the Local Group. It's not just the apparent faintness of stars at such large distances; the crowding of stars in a small patch of the sky is a more important problem.
How can astronomers figure out how severe this crowding problem is? Each side of a picture element (pixel) defines an angle on the sky, determined by the design of the instrument. Let's use something very small, like 0.1 arcsecond as our angle*.
If the galaxy is 5,000,000 parsecs away, you can use trigonometry to figure out that 0.1 arcsecond corresponds to ~2.5 parsecs. So each pixel covers 2.5 by 2.5 arcseconds (times the 'thickness' of the galaxy) - which is likely to contain several stars at least. This makes it more difficult to study individual objects!
* 1 arcsecond is a unit of angle that's 1/3600 of a degree. So, 0.1 arcsecond is 1/12,960,000 of a full circle. Knowing this, we can calculate that, at the distance of 5,000,000 parsecs (which is the radius of this circle), 0.1 arcsecond is about 2.5 parsecs.
Travel Time
If we traveled at 17.3 km/s, it would take us 40,000,000,000 (or 40 billion!) years to get to the nearest galaxy that is like our own - the Andromeda Galaxy! This travel time is longer than scientists believe the Universe has been around. If it were possible to travel at the speed of light, it would still take 2.3 million years to reach the Andromeda Galaxy.


