More On Uniform Circular Motion
(Credit: User Rept0n1x, via Wikimedia Commons)
Newton's First Law of motion states that an object moving at constant speed will continue that motion unless acted on by an outside force. This means that circular motion can only happen if there is a "center seeking" force – otherwise things would just travel in a straight line, rather than the curved line of a circule. Centripetal means 'center seeking', so centripetal force is used to refer to the force experienced by an object traveling in a circle. For example, when someone spins a ball attached to a rope horizontally above his head, the rope transmits a centripetal force from the muscles of the hand and arm, causing the ball to move in a circular path.
Centripetal forces cause centripetal accelerations. In the special case of the Earth's circular motion around the Sun – or any satellite's circular motion around any celestial body – the centripetal force causing the motion is the result of the gravitational attraction between them.
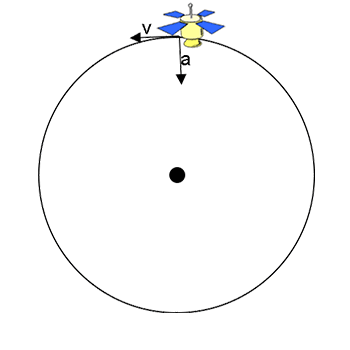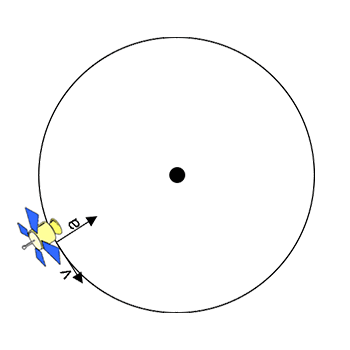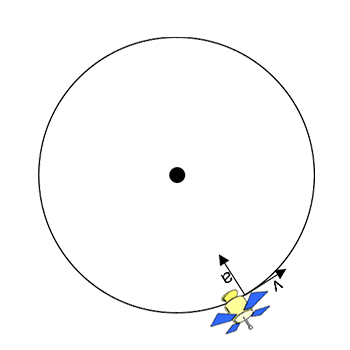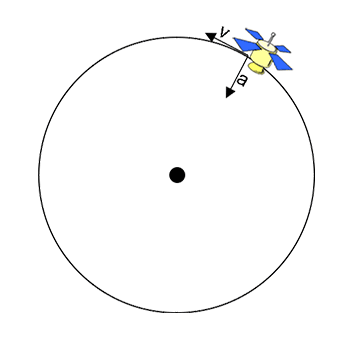
The arrows (or vectors) show the direction of the circular velocity (v, always tangent to the circular path) and the circular acceleration (a) caused by a centripetal force. Centripetal means center-seeking. Centripetal forces are always directed toward the center of the circular path.
By definition, acceleration is the rate of change in velocity of an object, and velocity is determined by dividing the distance travelled by the time interval it took to cover that distance. In the special case of circular motion, the distance covered is the circumference of a circle or 2πr, where π is the mathematical constant and r is the radius fo the circle. The time interval for an object to travel once around its circular path is called the period and is represented by T.
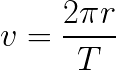
The equation for centripetal acceleration is:
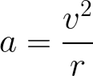
Putting those together, we get the equation for centripetal force:
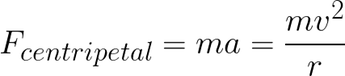
Take a quiz on uniform circular motion
Return to solving this using Newton's law of universal gravitation