NASA Insignia
Menu
Imagine the Universe!

Solving for the Mass of the Sun

The Sun
A brief outburst on the Sun as captured by the Solar Dynamics Observatory. (Credit: NASA SDO)

Because the gravitational attraction of our Sun for the Earth is the centripetal force causing the Earth's circular motion around the Sun, we can use Newton's law of universal gravitation to find the mass of the Sun without visiting the Sun. This is the same technique you would use to determine the mass of Cygnus X-1 with a probe. The Earth, orbiting the Sun, plays the same role as the probe sent to orbit Cygnus X-1.

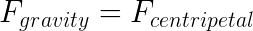
F_gravity = F_centripetal

From this, it follows that:

GMm/r^2=mv^2/r

The equation can be rearranged to solve for the mass of the Sun, M, by canceling the mass of the Earth, m, from both sides, and the orbital radius of the Earth, r. This leaves:

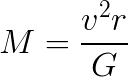
M=v^2r/G

In this equation, we know G, because it is a constant. However, we need to know how far the Earth is from the Sun and how fast it is moving around the Sun.

illustration of the Sun-earth orbital distance
  • The value for G is 6.67 × 10-11 N m2/kg2 (where N is Newtons)
  • The distance separating the Earth and the Sun (the orbital radius of the Earth around the Sun), r, is 1.5 × 108 km
  • The Earth's velocity around the Sun is just the total distance travelled divided by the time required for the Earth to make one complete orbit around the Sun, T
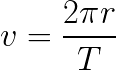
    v = (2)(pi)(r)/T

Make sure your distance measurement is in meters and your time measurement is in seconds in order for the units to cancel correctly.

x kg

More Information Return to solving this using Newton's law of universal gravitation

More Information Return to the beginning and try another approach