The Mathematics of the Relationship Between Intensity and Distance

If a galaxy is traveling away at a recession velocity V_r, then the increase in its distance from us during a time interval Δ t would simply be V_r × Δ t. If its intensity at a distance r is I₀, then the final intensity at the end of the time interval would be given by:

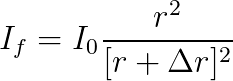
By convention, if the galaxy is moving away from us, V_r and therefore Δ r, is positive, and the intensity decreases, whereas if the galaxy is moving towards us Δ r is negative and the intensity increases. Substituting for Δ r we get

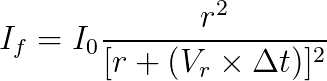
Expanding this out yields the functional form of the relationship between intensity and time for an object travelling at a speed V_r in terms of its velocity and the time elapsed:

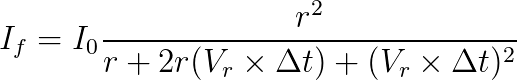
Looking at the expression in the denominator of this fraction, you can see that if the initial distance (r) is small compared to the distance the object travels in time Δ t, the expression reduces to:

If, on the other hand, the distance travelled in time Δ t is small compared to the initial distance of the object, the expression is approximately:

---

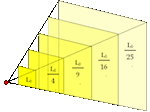
See another example of a 1/r² law

See a light curve for M31 and to try this technique to solve for its velocity.

Return to the beginning and try another approach