
The Local Group
About the Image
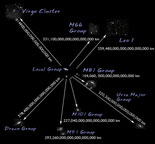
This is a compilation of actual images of the groups of galaxies that are in our Local Supercluster. They are shrunk down (though not to scale), and placed approximately correctly with respect to each other.
Clustering of galaxies seems to be the rule rather than the exception - about three quarters of all galaxies are in clusters. There are many small groups of galaxies, much like the Local Group, located relatively nearby. The giant, 2000-galaxy, Virgo Cluster is about 65 million light years away. It is the proximity of some 50 nearby small groups of galaxies to the Virgo cluster that suggests that they all form an enormous flattened cluster of clusters; we call it the Local Supercluster.
The Local Supercluster is actually centered on the Virgo Cluster of galaxies, which is why the Local Supercluster is sometimes called the Virgo Supercluster. Its equatorial plane is almost perpendicular to our Galactic plane. Our Supercluster, with a diameter measuring roughly 100 million light years or so, has a collective mass of about 1015 times the mass of the Sun.
The Local Group, which is near one edge of the Local Supercluster, appears to be revolving around its center at about 400 km/s.
Distance Information
The closest galaxy cluster to ours that is shown on this image is the M81 group located 104,060,000,000,000,000,000 km (11 million light years or 3.3 Mpc) away. The M101 group is 7.3 Mpc away, M51 is at 9.5 Mpc, M66 (Leo II) is 10.7 Mpc away, M96 (or Leo I) - 11.6 Mpc, NGC 5846, also known as the Draco group, is at 12.2 Mpc, and M109, the Ursa Major group, is 16.8 Mpc away.
How do We Calculate Distances of This Magnitude?
From the ground, we cannot use objects like Cepheid variables beyond distances of 5 Mpc (or 16.5 million light years) because they are too distant to distinguish their spectral types or periods. So what kind of objects can we use? Scientists use a variety of what are known as "standard candles" - that is, objects that are easily recognizable, and that have an intrinsic brightness that doesn't vary too much from one object to the next. Once an object is identified as a standard candle, an estimate of its luminosity can be made. Measurement of its apparent brightness and application of the inverse-square law allow its distance to be determined.
There are a large number of objects that have been used as standard candles - things like novae, HII regions, globular clusters, supernovae, and entire galaxies. Using objects like entire galaxies as standard candles gives us the capability to find distances to more and more distant objects.
Relationships like the Tully-Fisher relation (which says that the rotational velocity of a spiral galaxy is correlated with the total luminosity of the galaxy) are often called secondary distance indicators: they are very useful in measuring the relative distances to galaxies, but not very useful in pinning down the absolute values. Enter the Hubble Space Telescope: one of HST's key projects is to observe Cepheid variables in ~20 nearby galaxies, and to calibrate the secondary distance indicators. There is more information on this in the WMAP page on Hubble expansion.
Other methods that are used to find the distances to galaxies can be found on the ABCs of Distance pages.
Why Are These Distances Important To Astronomers?
In addition to the Hubble expansion (see above, and also the nearest superclusters page), the gravitational tug-of-war between individual galaxies, groups and clusters of galaxies influence the velocities of each other. For example, the Andromeda Galaxy is not receding from us like most galaxies, it is approaching towards the Milky Way! To establish the Hubble constant, you need to measure the velocities and the distances to galaxies at the edge of the Local Supercluster and beyond.
Travel Time
If we traveled at 17.3 km/s, it would take 191,000,000,000 years to arrive at the M81 group! If we traveled at the speed of light, it would still take 11 million years!


