Finding the variables

Recap: Your astronomy professor has tasked the class with determining the mass of the black hole candidate, Cygnus X-1. You thought of three possible ways to do this, one of which will give you the right answer. You've decided to try using Kepler's Laws.

Looking at the equation you found again:

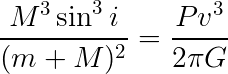
Where M and m are the masses of the binary stars, P is the orbital period, v is the orbital velocity of the object of mass m, i is the inclination of the orbit, π is a constant, and G is the gravitational constant (where G= 6.67 × 10^-11 m³ kg^-1 s^-2).

You quickly realize that for the problem at hand, M is the mass of the black hole, which is what your teacher asked you to find. So, you need to find or estimate values for m, the mass of the companion, P, v, and i.

The best way forward is to tackle them one at a time. Be sure to write down the values you find, so you are ready to solve the equation once you have all the variables ready.

• Find the orbital period, P, and velocity, v, of the black hole's companion.
• Find the inclination of the orbit relative to Earth, i.
• Find the mass of the black hole's companion, m.

Once you've measured or estimated all of the observables, you just need to solve the mass equation. It would help to rearrange the equation above to end up with a cubic equation of the form x³ + ax² + bx + c = 0, which can then be solved.

Get some help solving a cubic equation

Think you've got the answer? Enter it below and find out!

Get a bit more help solving the equation

Return to the beginning and try another approach