Getting started solving the cubic mass equation

Recap: Your astronomy professor has tasked the class with determining the mass of the black hole candidate, Cygnus X-1. You thought of three possible ways to do this, one of which will give you the right answer. You've decided to try using Kepler's Laws.

Start with the binary mass equation:

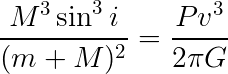
Then rearrange to get:

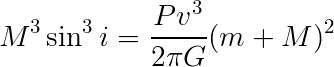
Then expand the right-hand side and rearrange to get this:

Now the equation is in the form of a cubic equation with:

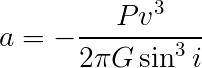
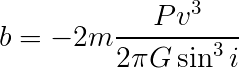
Notice that each of those has the following quantity:

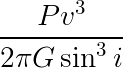
In fact, it will make things easier if we just define that:

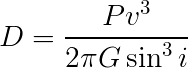
Then,

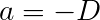
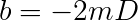
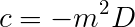
Using the following quantities, and converting to meters-kilograms-seconds units:

• i = 30^°
• P = 5.6 days = 4.8 × 10⁵ seconds
• v = 75 km/s = 7.5 × 10⁴ m/s
• m = 30 solar masses = 30 * (1.9 × 10^30 kg) = 5.7 × 10³¹

Your values might be a little different from those above – that's okay, as long as they aren't too far off. Substituting values in, then

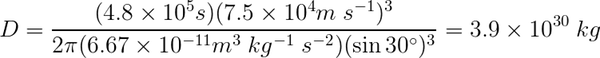
Numerically the values for the coefficients are:

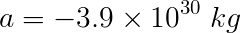
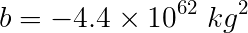
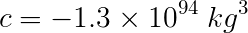
You are now ready to compute the quantities necessary to find the real cubic root (see Solving a Cubic Equation).

One additional hint: it will make things a lot simpler if you keep things in terms of solar masses. If you do, then,

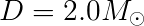
And,

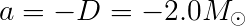
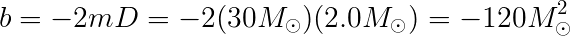
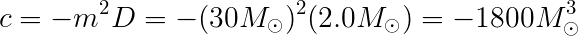
Then, just carry through those solar mass symbols through all of your calculations. The final answer is supposed to be in terms of solar mass anyway, and this way you don't have to deal with the huge exponents.

Return to enter your solution to the equation

Return to the beginning and try another approach