Using Kepler's Laws
You learned in class that it's generally not possible to determine the mass of a single star from its light alone. However, Cygnus X-1 is in a binary star system with a companion star, HDE 226868, a BO supergiant star. Being part of binary means that Cyg X-1 has a companion that it orbits. You recall that Kepler's Laws can be applied to any orbiting bodies, so perhaps you could use them to find the mass of Cyg X-1.
Going back to your astronomy text book, you refresh your memory of Kepler's Laws.
- Kepler's First Law, the law of orbits, states that all orbiting bodies move in elliptical orbits with the center of mass at one focus.
- Kepler's Second Law, the law of equal areas, states that the line between the stars (called the radius vector) sweeps out equal ares in equal periods of time.
- Kepler's Third Law, the law of periods, states that the square of the star's orbital period is proportional to the cube of its mean distance from the center of mass cubed.
Exploring your astronomy book a little further, you find the following equation tucked away in one of the "further reading" boxes:
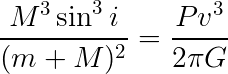
The box explains the variables in that equation as follows:
- M is the mass of the object of interest
- m is the mass of the companion object
- P is the orbital period
- v is the orbital velocity of the object of mass m
- i is the inclination of the orbit with respect to the observer
- G is the Gravitational Constant
The equation seems promising, if only you could figure out a few of those variables for Cygnus X-1 and its companion.
Learn about how that equation was derived
