Deriving the Doppler Shift
The mathematical relationships that describe the phenomenon of Doppler shift are relatively straightforward for objects moving much slower than the speed of light. Examine the picture below showing a wave traveling to the right with velocity v, wavelength lambda, and period T.
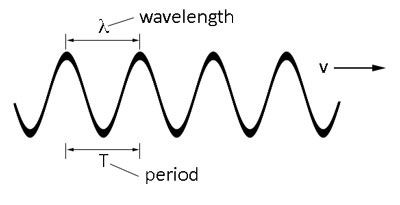
The period T, is the time it takes the wave to complete one cycle, or in other words, it is the time it takes for the wave to travel one wavelength. Since the velocity of the wave is the distance per time, we can write the velocity of the wave as:
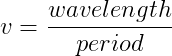
Since the period of a wave is the time it takes to complete one cycle, we can calculate the number of cycles in a given unit of time, called the wave frequency, by taking the inverse of the period.
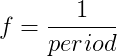
These two equations can be combined into what is called the universal wave equation:
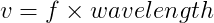
or
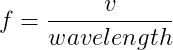
The actual and perceived frequency of the siren are the same so long as both are at rest and are given by the formula above. However, if the siren is moving towards the stationary observer, then the distance between successive wave crests is reduced by the distance traveled by the source during one period.
This resulting decreased wavelength called "lambda prime", or λ' in symbols. λ' is given by:
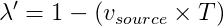
where
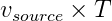
is equal to the distance traveled by the source in one period T.
The perceived frequency by the observer, which we will label f' must then be given by the following relationship:
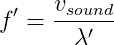
The observer behind the truck, on the other hand, perceives a decrease in the frequency and increase in wavelength of the siren. (Remember, the frequency of the siren is unchanged.) This is due to the fact that the source moves away and the distance between successive wave crests is increased due to the velocity of the source. As the siren is moves away from the stationary observer, the distance between successive wave crests is increased by the distance traveled by the source during one period.
Without much additional thought, you could easily convince yourself that the Doppler shift will occur under any of the following circumstances:
- The source is approaching a stationary observer.
- The observer is approaching a stationary source.
- The source and the observer are moving towards one another.
- The source is moving away from a stationary observer.
- The observer is moving away from a stationary source.
- The source and the observer are both moving away from each other.
- The source and the observer are moving in the same direction at different speeds.
You should also be able to easily convince yourself that the shift will yield an increase in the perceived frequency whenever the source and the observer are approaching one another and a decrease in the perceived frequency whenever the source and the observer are moving away from each other.
 See examples of redshifted spectra for some galaxies.
See examples of redshifted spectra for some galaxies.



