Doppler Shift
Play me a song about the Doppler Shift! (text)
Have you noticed that when an emergency vehicle with its siren blaring passes you that the tone that you hear changes in pitch? This is an example of the Doppler shift, and it is an effect that is associated with any wave phenomena (such as sound waves or light).
Consider a case where the firetruck is at rest in the fire station driveway waiting for the firemen to board, as shown in the image below. If the siren is on, a listener some distance away to the right will perceive the siren at the same frequency at which it is emitted. In fact, another stationary person on the left side of the truck would hear the same tone also.

(Credit: NASA's Imagine the Universe)
Now consider how this situation changes when the truck is moving towards the stationary observer with a constant velocity, v, as pictured below.

(Credit: NASA's Imagine the Universe)
The frequency of the fire engine's siren as heard by a person on the firetruck has not changed! However, the waves in the direction of the truck's motion bunch up as the fire truck is catching up to its own sound waves. The pressure variations, which are represented by the sine waves, impinge upon the eardrum of the stationary observer at an increased frequency. The stationary observer to the right therefore perceives a higher tone than the one actually emitted from the fire truck.
Notice that the waves behind the fire truck (on the left side of the diagram) are spread out because the siren is moving away from its own sound. This would cause a stationary observer to the left of the truck to perceive a decrease in the frequency of the of the siren.
For a source moving to the right, a stationary observer to the right would perceive a higher tone and one to the left would perceive a lower tone.
The non-relativistic Doppler shifted frequency of an object moving with speed v with respect to a stationary observer, is:
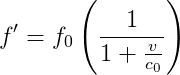
and the Doppler shifted wavelength can be shown to be:
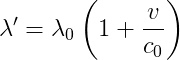
In these two equations, c0 is the speed of the wave in a stationary medium (the speed of sound in this case), and the velocity is the radial component of the velocity (the part in a straight line from the observer). Both these formulas are non-relativistic approximations that are true as long as the velocity of the moving object is much less than the speed of light.
As a convention, the velocity is positive if the source is moving away from us and negative if the source is moving towards the observer.
Thus:
- if the source is moving away (positive velocity) the observed frequency is lower and the observed wavelength is greater (redshifted).
- if the source is moving towards (negative velocity) the observed frequency is higher and the wavelength is shorter (blueshifted).
How does this affect the spectra of distant objects in the Universe? Does light experience the Doppler shift?
Think about the spectrum of visible light: red-orange-yellow-green-blue-indigo-violet (or ROY G. BIV for short). If the Doppler shift also works for light then it must be possible to move so quickly towards a red traffic light that it would appear green to you! You might find it clever to use this argument if you get stopped for running a red light. However, the police officer might then give you a ticket for speeding.
It turns out that light from any part of the electromagnetic spectrum can be shifted up or down in frequency depending upon your relative motion to the emitting source. The following diagram illustrates this phenomenon:
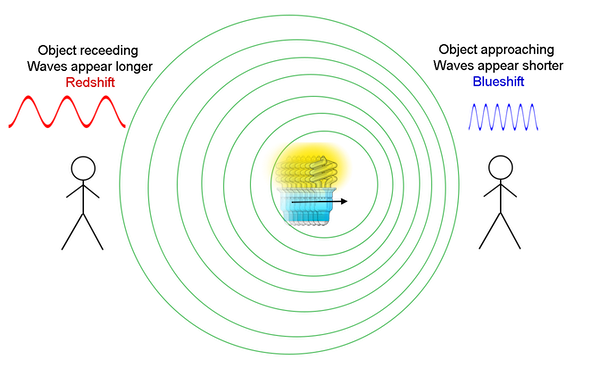
(Credit: NASA's Imagine the Universe)
You will recognize this as a similar diagram to the one showing a fire truck approaching the stationary observer, except now the source is emitting light instead of sound. Notice that the region where an observer perceives an increase in the frequency of light is referred to as "blueshifted", and the region where the observer would perceive a lower frequency (on the left in the diagram) is referred to as "redshifted." And, it is important to note that the equations derived for the Doppler shift of sound work equally well for moving light sources provided the light sources are not moving near the speed of light. If the relative velocity between the emitting source and the observer was close to the speed of light, we would have to take relativistic effects into account; thus, the equation would change.
 See a mathematical derivation of the Doppler shift equation.
See a mathematical derivation of the Doppler shift equation.
 See examples of redshifted spectra for some galaxies.
See examples of redshifted spectra for some galaxies.




